题目内容
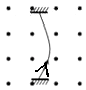
【题目】如图所示，光滑水平地面与足够长的倾角θ＝30°的光滑斜面平滑连接，A球位于斜面底端，B球在水平地面上，两者相距L＝10 m．现A、B两个小球均以初速度v0＝10m/s开始运动，A沿斜面向上，B沿水平面向右，取g＝10m/s2，求：
(1)B球刚要滑上斜面时A球的速度；
(2)A球到达最高点时，AB两球之间的距离．
【答案】（1）5m/s（2）2.5m
【解析】(1)设B球经过t1时间到达斜面底端，有：t1＝
＝1 s
A球在斜面上运动的加速度大小为a，由牛顿第二定律得：
a＝
＝mgsin30°＝5m/s
由v1＝v0－at1 得B球到达斜面底端时A球的速度为v1＝10－5×1＝5 m/s
(2)A球到达斜面顶端的距离为
sA＝
＝
＝10 m
A球在斜面上滑行t2速度减为零
t2＝
＝2 s
B球在斜面上滑行距离sB＝v0(t2－t1)－
a(t2－t1)2＝7.5 m
故A与B相距 Δs＝sA－sB＝2.5 m
练习册系列答案
相关题目
