题目内容
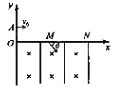
【题目】如图所示,BCD是光滑绝缘的半圆形轨道,位于竖直平面内,直径BD竖直轨道半径为R,下端与水平绝缘轨道在B点平滑连接,质量为m的不带电的滑块b静止在B点整个轨道处在水平向左的匀强电场中场强大小为E.质量为m、带正电的小滑块a置于水平轨道上,电荷量为![]() ,滑块a与水平轨道间的动摩擦因数μ=0.5,重力加速度为g。现将滑块a从水平轨道上距离B点12R的A点由静止释放,运动到B点与滑块b碰撞,碰撞时间极短且电量不变,碰后两滑块粘在一起运动,a、b滑块均视为质点。求:
,滑块a与水平轨道间的动摩擦因数μ=0.5,重力加速度为g。现将滑块a从水平轨道上距离B点12R的A点由静止释放,运动到B点与滑块b碰撞,碰撞时间极短且电量不变,碰后两滑块粘在一起运动,a、b滑块均视为质点。求:

(1)滑块a、b碰撞后的速度大小。
(2)滑块在圆形轨道上最大速度的大小,以及在最大速度位置处滑块对轨道作用力的大小。
(3)滑块第一次落地点到B点的距离。
【答案】(1)滑块a、b碰撞后的速度大小分别为![]() 和
和![]()
(2)滑块在圆形轨道上最大速度的大小为![]() ,以及在最大速度位置处滑块对轨道作用力的大小为
,以及在最大速度位置处滑块对轨道作用力的大小为![]() 。
。
(3)滑块第一次落地点到B点的距离为(![]() )R。
)R。
【解析】
(1)a从A到B的过程用动能定理得![]() ,解得
,解得![]() 对a与b碰撞用动量守恒定律得mv1=2mv2,解得
对a与b碰撞用动量守恒定律得mv1=2mv2,解得![]()
(2)当滑块重力与电场力合力方向和圆轨道径向一致时,滑块速度最大。如图,则有![]() ,对滑块从碰后到最大速度的过程用动能定理有
,对滑块从碰后到最大速度的过程用动能定理有![]() ,解得滑块最大速度
,解得滑块最大速度![]() ,滑块在P点用牛顿第二定律得,
,滑块在P点用牛顿第二定律得,![]() ,解得滑块受到轨道支持力
,解得滑块受到轨道支持力![]() ,由牛顿第三定律。此时滑块对轨道作用力
,由牛顿第三定律。此时滑块对轨道作用力![]()
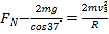
(3)a、b整体从B到D的过程中。由动能定理有![]() ,解得
,解得![]() ,在D点。对滑块受力分析得:
,在D点。对滑块受力分析得:![]() ,解得
,解得![]() ,所以滑块能通过D点接着水平飞出,在竖直方向;
,所以滑块能通过D点接着水平飞出,在竖直方向;![]() ,解得
,解得![]() 水平方问受电场力加速度不变则
水平方问受电场力加速度不变则![]()

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目