题目内容
16.质量为2×103kg,发动机额定功率为80kW的汽车在平直公路上行驶;若汽车所受阻力大小恒为重力的0.2倍,则下列判断中正确的有( )| A. | 汽车的最大动能是4×104J | |
| B. | 汽车以加速度2 m/s2从静止开始匀加速启动,启动后第2秒末时发动机实际功率是32 kW | |
| C. | 若汽车保持额定功率启动,则当汽车速度为8m/s时,其加速度为3 m/s2 | |
| D. | 汽车以加速度2 m/s2从静止开始的匀加速启动中,达到最大速度时摩擦力做功为4×105 J |
分析 当牵引力等于阻力时,速度最大,根据P=Fv求出最大速度,从而得出汽车的最大动能;根据牛顿第二定律求出匀加速直线运动的牵引力,结合P=Fv求出匀加速直线运动的最大速度,从而得出匀加速直线运动的时间,判断汽车功率是否达到额定功率,再根据速度时间公式求出速度的大小,结合P=Fv求出实际功率.根据P=Fv求出速度为5m/s时的牵引力,结合牛顿第二定律求出汽车的加速度
解答 解:A、汽车的最大速度为:${v}_{m}=\frac{P}{f}=\frac{80000}{0.2×2000×10}m/s=20m/s$,则汽车的最大动能为:${E}_{km}=\frac{1}{2}{mv}_{m}^{2}=\frac{1}{2}×2000×2{0}^{2}J=4×1{0}^{5}$J,故A正确.
B、根据牛顿第二定律得牵引力为:F=f+ma=4000+2000×2N=8000N,则匀加速直线运动的最大速度为:${v}_{1}=\frac{P}{F}=\frac{80000}{8000}m/s=10m/s$,可知匀加速直线运动的时间为:t=$\frac{{v}_{1}}{a}=\frac{10}{2}s=5s$,2s末的速度为:v=at2=2×2m/s=4m/s,则发动机的实际功率为:P=Fv=8000×4W=32kW,故B正确.
C、当速度为8m/s时,汽车的牵引力为:F=$\frac{P}{v}=\frac{80000}{8}N=10000N$,根据牛顿第二定律得加速度为:a=$\frac{F-f}{m}=\frac{10000-0.2×2000×10}{2000}m/{s}^{2}=3m/{s}^{2}$,故C正确;
D、从静止开始的匀加速启动中,达到最大速度时,通过的位移x=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×2×{5}^{2}m=25m$,摩擦力做功${W}_{f}=-fx=-4000×25J=-1×1{0}^{5}J$,故D错误
故选:ABC
点评 解决本题的关键会通过汽车受力情况判断其运动情况,知道汽车在平直路面上行驶时,当牵引力与阻力相等时,速度最大

 名校课堂系列答案
名校课堂系列答案
| A. | 这列波的波速是25m/s | |
| B. | 在X=100m处有一接收器接收到的频率变大 | |
| C. | 经过△t=0.4s,A质点通过的路程是2cm | |
| D. | 质点P将比质点Q先回到平衡位置 |
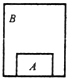 如图,物体A静止在箱子B中,离地足够高,某时刻将它们由静止自由释放,则在下落过程中,下列说法正确的是( )
如图,物体A静止在箱子B中,离地足够高,某时刻将它们由静止自由释放,则在下落过程中,下列说法正确的是( )| A. | 若没有空气阻力,A开始的一段短时间内,速度增加得越来越快 | |
| B. | 若没有空气阻力,A所受的支持力始终为零 | |
| C. | 若空气阻力与速度成正比,则开始的一段短时间内,A受的支持力越来越大 | |
| D. | 若空气阻力与速度成正比,只要下落时间足够长,则A可能不受B的支持力而“飘”起来 |
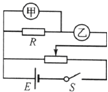
| A. | 甲是电流表,乙是电压表 | B. | 甲是电压表,乙是电流表 | ||
| C. | 电阻R两端电压可以为零 | D. | 流过变阻器的电流可以为零 |
| A. | 所谓超导体,当其温度降低到接近绝对零度的某个临界温度时,电阻率突然变为零 | |
| B. | 各种材料的电阻率都与温度有关,金属的电阻率随温度升高而增大 | |
| C. | 电阻率是表征材料导电性能好坏的物理量,电阻率越大,其导电性能越好 | |
| D. | 某些合金的电阻率几乎不受温度变化的影响,通常都用它们制作标准电阻 |
 如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了10J,金属块克服摩擦力做功大小6J,重力做功18J,则以下判断正确的是( )
如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了10J,金属块克服摩擦力做功大小6J,重力做功18J,则以下判断正确的是( )| A. | 金属块带负电荷 | |
| B. | 静电力做功-2J | |
| C. | 金属块的电势能与动能之和增加了12 J | |
| D. | 金属块的机械能减少10 J |
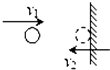 如图所示小球以v1=4m/s的速度水平向右运动,碰到墙壁经△t=0.1s后以v2=3m/s的速度沿同一直线反弹.小球在这0.1s内的加速度为( )
如图所示小球以v1=4m/s的速度水平向右运动,碰到墙壁经△t=0.1s后以v2=3m/s的速度沿同一直线反弹.小球在这0.1s内的加速度为( )| A. | 10m/s2,方向向右 | B. | 10m/s2,方向向左 | C. | 70m/s2,方向向右 | D. | 70m/s2,方向向左 |
| A. | 汽车匀速直线爬坡 | |
| B. | 气球被风刮着水平向东匀速飘移 | |
| C. | 火车沿水平面内的弯曲轨道匀速前进 | |
| D. | 航天飞机的返回舱着地前斜向下匀速降落 |