题目内容
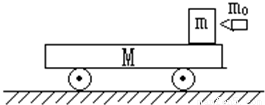
如图，在光滑水平面上有一辆质量M=6Kg的平板小车，车上的质量为m=1.96Kg的木块，木块与小车平板间的动摩擦因数μ=0.3，车与木块一起以V=2m/s的速度向右行驶．一颗质量m=0.04Kg的子弹水平速度v=98m/s，在很短的时间内击中木块，并留在木块中（g=10m/s2）（1）如果木块刚好不从平板车上掉下来，小车L多长？
（2）如果木块刚好不从车上掉下来，从子弹击中木块开始经过1.5s木块的位移是多少？
【答案】分析：（1）子弹射入木块，子弹和木块系统内力远大于外力，动量守恒；子弹、木块和木板系统动量也守恒；根据动量守恒定律和功能关系列方程，联立后解出小车的长度；
（2）先根据牛顿第二定律求出木块和木板的加速度，然后根据运动学公式列式分析求解．
解答：解：（1）子弹射入木块，子弹和木块系统内力远大于外力，动量守恒，有：mv-mv=（m+m）v1 …①
解得
v1=0
若它们相对平板车滑行L，则它们恰好不从小车上掉下来，它们跟小车有共同速度V′，根据动量守恒定律，有
Mv=（m+m+M）v′…②
解得
v′=1.5m/s
由能量守恒定律有：
Q=μ（m+m）g L=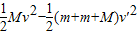
…③
由①②③，代入数据可求出：L=0.5m
即要使木块不掉下来，小车L的长度为0.5m．
（2）子弹射入木块后，木块在摩擦力的作用下做匀加速直线运动，根据牛顿第二定律，滑块的加速度：a=μg=3m/s2．
经过时间t1速度为v′，有v′=at1
解得：t1=0.5s．
在这段时间内，木块做匀加速运动，通过的位移：S1=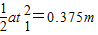
在t2=t-t1=1s内做匀速运动，通过位移为：s2=v′t2=1.5m．
故在3S内的总位移S总=S1+S2=1.875m．
点评：本题关键要分析求出小木块和长木板的运动情况，然后根据动量守恒定律、功能关系、牛顿第二定律、运动学公式联立方程组求解．
（2）先根据牛顿第二定律求出木块和木板的加速度，然后根据运动学公式列式分析求解．
解答：解：（1）子弹射入木块，子弹和木块系统内力远大于外力，动量守恒，有：mv-mv=（m+m）v1 …①
解得
v1=0
若它们相对平板车滑行L，则它们恰好不从小车上掉下来，它们跟小车有共同速度V′，根据动量守恒定律，有
Mv=（m+m+M）v′…②
解得
v′=1.5m/s
由能量守恒定律有：
Q=μ（m+m）g L=
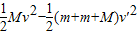…③由①②③，代入数据可求出：L=0.5m
即要使木块不掉下来，小车L的长度为0.5m．
（2）子弹射入木块后，木块在摩擦力的作用下做匀加速直线运动，根据牛顿第二定律，滑块的加速度：a=μg=3m/s2．
经过时间t1速度为v′，有v′=at1
解得：t1=0.5s．
在这段时间内，木块做匀加速运动，通过的位移：S1=
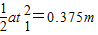
在t2=t-t1=1s内做匀速运动，通过位移为：s2=v′t2=1.5m．
故在3S内的总位移S总=S1+S2=1.875m．
点评：本题关键要分析求出小木块和长木板的运动情况，然后根据动量守恒定律、功能关系、牛顿第二定律、运动学公式联立方程组求解．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
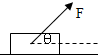如图，在光滑水平面上有一质量为m的物体，在与水平方向成θ角的恒定拉力F作用下运动，则在时间t内（ ）| A、重力的冲量为0 | B、拉力F的冲量为Ft | C、拉力F的冲量为Ftcosθ | D、拉力F的冲量等于物体动量的变化量 |
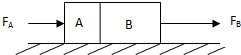如图，在光滑水平面上放着紧靠在一起的A、B两物体，B的质量是A的2倍，B受到向右的恒力FB=2N，A受到的水平力FA=（9-2t）N（t的单位是s），从t=0开始计时，则下列说法不正确的是（ ）
如图，在光滑水平面上放着质量分别为m和2m的A、B两个物块，现用外力缓慢向左推B使弹簧压缩，此过程中推力做功W．然后撤去外力，则（ ）
如图，在光滑水平面上，有一竖直向下的匀强磁场，分布在宽度为L的区域内，现有一边长为l（l＜L）的正方形闭合导线框以垂直磁场边界的初速度v1滑进磁场，然后线圈滑出磁场的速度为v2，设线框滑进磁场的时间为t1，安接力的冲量为I1，线框产生的热量为Q1，线框滑出磁场的时间为t2，安培力的冲量为I2，线框产生的热量为Q2，则有（ ）