题目内容
9.汽车启动的快慢和能够达到的最大速度,是衡量汽车性能体系中的两个重要指标.汽车启动的快慢用车的速度从0到20m/s加速时间来表示,这个时间越短,汽车启动的加速度就越大.表中列出了两种汽车的最佳性能指标:| 启动的快慢(s)(0~20m/s的加速时间) | 最大速度/m•s-1 | |
| 甲车 | 8 | 30 |
| 乙车 | 4 | 40 |
(1)两车相遇时甲车行驶的路程是多少?
(2)甲车先于乙车起动的时间t0.
分析 (1)根据加速度的定义求甲乙的加速度,结合速度时间公式求加速到最大速度所需的时间.(2)根据位移公式求出乙车的位移,以及加速运动通过的位移,然后可判断甲乙在甲匀速阶段相遇,最后利用位移关系、时间关系求出甲乙相遇时甲通过的位移,以及甲先于乙运动的时间.
解答 解:(1)由两车的性能指标,可知,甲车的最大加速度为:${a}_{甲}=\frac{20}{8}m/{s}^{2}=2.5m/{s}^{2}$,乙车的最大加速度为:${a}_{乙}=\frac{20}{4}m/{s}^{2}=5m/{s}^{2}$,所以,甲车由静止加速的最大加速时间为:${t}_{甲}=\frac{{v}_{甲m}}{{a}_{甲}}=\frac{30}{2.5}=12s$,甲加速运动行驶的位移:${x}_{甲}=\frac{1}{2}{a}_{甲}{{t}_{甲}}^{2}=180m$,乙车由静止加速的最大加速时间为:${t}_{乙}=\frac{{v}_{乙m}}{{a}_{乙}}=\frac{40}{5}s=8s$,故乙车开出8s恰好达到最大速度,通过的位移为${x}_{乙}=\frac{{{v}_{乙m}}^{2}}{2{a}_{乙}}=160m$,因为x甲<x乙+110m,故甲乙在匀速运动阶段与乙相遇,甲匀速运动通过的位移△x=110m+160m-180m=90m.故甲与乙相遇时甲行驶的位移为:x甲′=x甲+△x=180m+90m=270m.
(2)甲匀速运动的时间$△t=\frac{90}{30}s=3s$,故甲车先于乙车起动的时间t0=t甲+△t-t乙=7s.
点评 本题属于追击问题,解题的关键是分清物理过程,抓住相遇时通过的位移相等这一关键点,建立关系式,结合有关运动学公式解之即可.

| A. | 周期性变化的电磁场由近及远地向周围传播就形成了电磁波 | |
| B. | 电磁场是一种特殊物质,不能在真空中传播 | |
| C. | 电磁波的速度总是3×108m/s | |
| D. | 磁场在周围空间总会激发电场 |
 如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.无人机的质量为m=2kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始,以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m,g取10m/s2.求:
如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.无人机的质量为m=2kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始,以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m,g取10m/s2.求: 在用单摆测定重力加速度实验中:
在用单摆测定重力加速度实验中: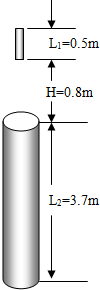 如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m.直杆位于 圆筒正上方H=0.8m处.直杆从静止开始做自由落体运动,并能竖直穿越圆筒.试求(取g=10m/s2)
如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m.直杆位于 圆筒正上方H=0.8m处.直杆从静止开始做自由落体运动,并能竖直穿越圆筒.试求(取g=10m/s2)
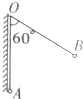 如图所示,真空中两条长为60cm的丝线一端固定于0点,另一端分别系一质量为0.1g的小球A和B.当两小球带相同的电荷量时,A球被光滑的绝缘挡板挡住,且使0B线保持与竖直方向成60°角而静止.取g=10m/s2.
如图所示,真空中两条长为60cm的丝线一端固定于0点,另一端分别系一质量为0.1g的小球A和B.当两小球带相同的电荷量时,A球被光滑的绝缘挡板挡住,且使0B线保持与竖直方向成60°角而静止.取g=10m/s2. 在20m高的楼房顶上,将一个质量为m的小球以5m/s的速度水平抛出,如图所示,小球在水平方向运动10m时,在竖直方向运动了20m,你认为应该建立怎样的坐标才能方便地描述小球现在所处的位置?按你所建立的坐标系,写出小球现在的位置坐标.
在20m高的楼房顶上,将一个质量为m的小球以5m/s的速度水平抛出,如图所示,小球在水平方向运动10m时,在竖直方向运动了20m,你认为应该建立怎样的坐标才能方便地描述小球现在所处的位置?按你所建立的坐标系,写出小球现在的位置坐标.