题目内容
3.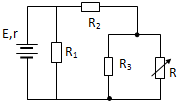 如图所示的电路,电源电动势为E,内电阻为r,R为一电阻箱.R1、R2、R3均为定值电阻,当电阻箱R的阻值减小时( )
如图所示的电路,电源电动势为E,内电阻为r,R为一电阻箱.R1、R2、R3均为定值电阻,当电阻箱R的阻值减小时( )| A. | R1的功率增大 | B. | 电源的总功率减小 | ||
| C. | R3中电流增大 | D. | R中电流增大 |
分析 当R的电阻减小时,R3和R的并联电阻减小,R2所在支路电阻减小,外电路总电阻减小,根据闭合电路欧姆定律分析总电流会增大,电源的总功率增大.结合部分电路欧姆定律和串并联关系分析各个支路电流的变化.
解答 解:A、当R的电阻减小时,R3和R的并联电阻减小,R2所在支路电阻减小,外电路总电阻减小,根据闭合电路欧姆定律得,流过电源的电流变大,故内电压表大,路端电压减小,则R1的电压减小,故R1的功率减小,故A错误;
B、由于总电流增大,由P=EI知,电源的总功率增大,故B错误.
C、路端电压减小,R1的电流减小,总电流增大,R2中电流增大,故R2电压增大,故R3两端电压减小,通过R3的电流减小,故C错误;
D、R2中电流增大,R3两端电压减小,通过R3的电流减小,故R中电流增大,故D正确.
故选:D
点评 本题按“部分→整体→部分”的思路进行动态变化分析.对于电压表的示数,可以直接根据路端电压随外电阻而增大的结论进行分析.

练习册系列答案
相关题目
14.假设地球可视为质量均匀分布的球体.地球表面处的重力加速度大小为g0,与地球表面相距为h处的重力加速度大小为g1.忽略地球自转,引力常量为G.则地球的质量为( )
| A. | $\frac{{h}^{2}}{G}$$\frac{{g}_{0}}{{g}_{0}-{g}_{1}}$ | B. | $\frac{{h}^{2}}{G}$$\frac{{g}_{0}{g}_{1}}{({g}_{0}-{g}_{1})^{2}}$ | ||
| C. | $\frac{{h}^{2}}{G}$$\frac{{g}_{0}{g}_{1}}{(\sqrt{{g}_{0}-\sqrt{{g}_{1}}})^{2}}$ | D. | $\frac{{h}^{2}}{G}$$\frac{\sqrt{{g}_{0}{g}_{1}}}{\sqrt{{g}_{0}}-\sqrt{{g}_{1}}}$ |
11.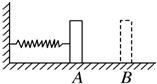 如图所示,一轻质弹簧两端分别与竖直墙壁和物块连接,物块位于水平面上.A、B是物块能保持静止的位置中离墙壁最近和最远的点,A、B两点离墙壁的距离分别是x1、x2.物块与地面的最大静摩擦力为Ffm,则弹簧的劲度系数为( )
如图所示,一轻质弹簧两端分别与竖直墙壁和物块连接,物块位于水平面上.A、B是物块能保持静止的位置中离墙壁最近和最远的点,A、B两点离墙壁的距离分别是x1、x2.物块与地面的最大静摩擦力为Ffm,则弹簧的劲度系数为( )
 如图所示,一轻质弹簧两端分别与竖直墙壁和物块连接,物块位于水平面上.A、B是物块能保持静止的位置中离墙壁最近和最远的点,A、B两点离墙壁的距离分别是x1、x2.物块与地面的最大静摩擦力为Ffm,则弹簧的劲度系数为( )
如图所示,一轻质弹簧两端分别与竖直墙壁和物块连接,物块位于水平面上.A、B是物块能保持静止的位置中离墙壁最近和最远的点,A、B两点离墙壁的距离分别是x1、x2.物块与地面的最大静摩擦力为Ffm,则弹簧的劲度系数为( )| A. | $\frac{Ffm}{{x}_{1}+{x}_{2}}$ | B. | $\frac{2Ffm}{{x}_{1}+{x}_{2}}$ | C. | $\frac{2Ffm}{{x}_{2}-{x}_{1}}$ | D. | $\frac{Ffm}{{x}_{2}-{x}_{1}}$ |
8.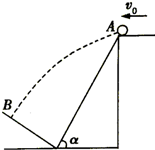 如图所示,一小球以速度v0从倾角为的斜面顶端A处水平抛出,垂直落到在斜面底端与斜面垂直的挡板上的B点,已知重力加速度为g,则下列说法正确的是( )
如图所示,一小球以速度v0从倾角为的斜面顶端A处水平抛出,垂直落到在斜面底端与斜面垂直的挡板上的B点,已知重力加速度为g,则下列说法正确的是( )
 如图所示,一小球以速度v0从倾角为的斜面顶端A处水平抛出,垂直落到在斜面底端与斜面垂直的挡板上的B点,已知重力加速度为g,则下列说法正确的是( )
如图所示,一小球以速度v0从倾角为的斜面顶端A处水平抛出,垂直落到在斜面底端与斜面垂直的挡板上的B点,已知重力加速度为g,则下列说法正确的是( )| A. | 可求A、B之间的距离 | |
| B. | 可求小球落到B点时速度的大小和方向 | |
| C. | 可求小球到达B点时的动能 | |
| D. | 可以断定,当小球速度方向与斜面平行时,小球与斜面间的距离最大 |
15. 为测量一轻质弹簧的劲度系数,某同学进行了如下实验:先将弹簧竖直悬挂,而后在弹簧下端挂上重为6N的钩码,弹簧静止时的位置如图所示,可求得该弹簧的劲度系数为( )
为测量一轻质弹簧的劲度系数,某同学进行了如下实验:先将弹簧竖直悬挂,而后在弹簧下端挂上重为6N的钩码,弹簧静止时的位置如图所示,可求得该弹簧的劲度系数为( )
 为测量一轻质弹簧的劲度系数,某同学进行了如下实验:先将弹簧竖直悬挂,而后在弹簧下端挂上重为6N的钩码,弹簧静止时的位置如图所示,可求得该弹簧的劲度系数为( )
为测量一轻质弹簧的劲度系数,某同学进行了如下实验:先将弹簧竖直悬挂,而后在弹簧下端挂上重为6N的钩码,弹簧静止时的位置如图所示,可求得该弹簧的劲度系数为( )| A. | 20 N/m | B. | 30 N/m | C. | 60N/m | D. | 120 N/m |
13.如图所示为两电源的U-I图象,则下列说法正确的是( )
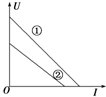

| A. | 电源①的电动势和内阻均比电源②大 | |
| B. | 当外接相同的电阻时,两电源的输出功率可能相等 | |
| C. | 不论外接多大的相同电阻,电源①的输出功率总比电源②的输出功率大 | |
| D. | 当外接同样的电阻时,两电源的效率可能相等 |
 如图所示的是某种手机电池上的文字说明,请仔细阅读,并根据所给数据求解以下列问题:
如图所示的是某种手机电池上的文字说明,请仔细阅读,并根据所给数据求解以下列问题: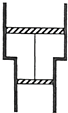 如图,一固定的竖直气缸有一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为m1=2.50kg,横截面积为s1=80.0cm2,小活塞的质量为m2=1.50kg,横截面积为s2=40.0cm2;两活塞用刚性轻杆连接,间距保持为l=40.0cm,气缸外大气压强为p=1.00×105Pa,温度为T=360K.初始时大活塞与大圆筒底部相距$\frac{l}{2}$,两活塞间封闭气体的温度为T1=510K,现气缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与气缸壁之间的摩擦,重力加速度g取10m/s2.求
如图,一固定的竖直气缸有一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为m1=2.50kg,横截面积为s1=80.0cm2,小活塞的质量为m2=1.50kg,横截面积为s2=40.0cm2;两活塞用刚性轻杆连接,间距保持为l=40.0cm,气缸外大气压强为p=1.00×105Pa,温度为T=360K.初始时大活塞与大圆筒底部相距$\frac{l}{2}$,两活塞间封闭气体的温度为T1=510K,现气缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与气缸壁之间的摩擦,重力加速度g取10m/s2.求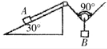 如图所示,斜面的倾角为30°放在水平面上,轻绳通过两个滑轮于A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦,物块A的质量为m,且与斜面间的动摩擦因数为μ,不计滑轮的质量,挂在物块B后,当动滑轮两边轻绳的夹角为90°时,A,B恰能保持静止,整个装置处于静止状态,重力加速度为g,最大静摩擦近似等于滑动摩擦.求:
如图所示,斜面的倾角为30°放在水平面上,轻绳通过两个滑轮于A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦,物块A的质量为m,且与斜面间的动摩擦因数为μ,不计滑轮的质量,挂在物块B后,当动滑轮两边轻绳的夹角为90°时,A,B恰能保持静止,整个装置处于静止状态,重力加速度为g,最大静摩擦近似等于滑动摩擦.求: