题目内容
12.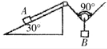 如图所示,斜面的倾角为30°放在水平面上,轻绳通过两个滑轮于A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦,物块A的质量为m,且与斜面间的动摩擦因数为μ,不计滑轮的质量,挂在物块B后,当动滑轮两边轻绳的夹角为90°时,A,B恰能保持静止,整个装置处于静止状态,重力加速度为g,最大静摩擦近似等于滑动摩擦.求:
如图所示,斜面的倾角为30°放在水平面上,轻绳通过两个滑轮于A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦,物块A的质量为m,且与斜面间的动摩擦因数为μ,不计滑轮的质量,挂在物块B后,当动滑轮两边轻绳的夹角为90°时,A,B恰能保持静止,整个装置处于静止状态,重力加速度为g,最大静摩擦近似等于滑动摩擦.求:(1)物块B的质量为多少时,A与斜面恰好没有摩擦力作用;
(2)A与斜面恰好没有摩擦力作用时,水平地面对斜面的摩擦力为多大;
(3)物块B的质量满足什么条件时,物块A能在斜面上保持静止.
分析 (1)当A与斜面恰好没有摩擦力作用时,A受到重力、斜面的支持力和绳子的拉力,根据平衡条件求出绳子的拉力,再C对滑轮研究,由平衡条件求B的质量.
(2)对斜面和A整体研究,由平衡条件求解水平地面对斜面的摩擦力.
(3)当A刚要下滑时B的质量最小,当A刚好上滑时B的质量最大,A刚要滑动时静摩擦力达到最大值,根据平衡条件解答.
解答 解:(1)当A与斜面间的摩擦力Ff=0N时,A受到重力、斜面的支持力和绳子的拉力,则得绳子的拉力
T=mgsin30°=0.5mg
对于滑轮有:$\sqrt{2}$T=mBg
可得 mB=$\frac{\sqrt{2}}{2}$m
(2)对斜面和A整体研究,由平衡条件得:
水平方向有:f=Tcos45°=$\frac{\sqrt{2}}{2}$mg
(3)解:以A为研究对象,受力分析,如图,当B的质量最大时,A有向上的运动趋势,静摩擦力达到最大.
根据共点力平衡条件,有:
mgsin30°+fm=T
N=mgcos30°
又 fm=μN
联立得:T=$\frac{1+\sqrt{3}μ}{2}$mg
以动滑轮为研究对象,有:
mBg=$\sqrt{2}$T
解之得:mB=$\frac{\sqrt{2}+\sqrt{6}μ}{2}$m
同理,当A刚要下滑时b的质量最小,A所受的静摩擦力沿斜面向上达到最大,则有:
mgsinα=μmgcosα+T′
以动滑轮为研究对象,有:mB′g=$\sqrt{2}$T′
联立解得 mB′=$\frac{\sqrt{2}-\sqrt{6}μ}{2}$m
故要保证物块A能在斜面上保持静止,B的质量范围为:$\frac{\sqrt{2}-\sqrt{6}μ}{2}$m≤mB≤$\frac{\sqrt{2}+\sqrt{6}μ}{2}$m.
答:(1)物块B的质量为$\frac{\sqrt{2}}{2}$m时,A与斜面恰好没有摩擦力作用;
(2)A与斜面恰好没有摩擦力作用时,水平地面对斜面的摩擦力为$\frac{\sqrt{2}}{2}$mg;
(3)物块B的质量满足条件为:$\frac{\sqrt{2}-\sqrt{6}μ}{2}$m≤mB≤$\frac{\sqrt{2}+\sqrt{6}μ}{2}$m时,物块A能在斜面上保持静止.
点评 解决本题的关键要把握物体刚要滑动的临界条件:静摩擦力达到最大值,灵活选取研究对象,抓住A与滑轮之间的联系:绳子,由平衡条件和摩擦力公式解答.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 除永久磁铁外,一切磁场都是由运动电荷产生的 | |
| B. | 一切磁现象都起源于运动电荷 | |
| C. | 一切磁作用都是运动电荷通过磁场而产生 | |
| D. | 所有的磁现象都可以归结为运动电荷对运动电荷的作用 |
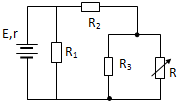 如图所示的电路,电源电动势为E,内电阻为r,R为一电阻箱.R1、R2、R3均为定值电阻,当电阻箱R的阻值减小时( )
如图所示的电路,电源电动势为E,内电阻为r,R为一电阻箱.R1、R2、R3均为定值电阻,当电阻箱R的阻值减小时( )| A. | R1的功率增大 | B. | 电源的总功率减小 | ||
| C. | R3中电流增大 | D. | R中电流增大 |
| A. | 作用在物体上的静摩擦力可以是动力 | |
| B. | 摩擦力的大小一定与物体的重力成正比 | |
| C. | 运动的物体不可能受到静摩擦力作用 | |
| D. | 作用在物体上的滑动摩擦力只能使物体减速,不可能使物体加速 |

| A. | t=3s时,物体C追上物体D | |
| B. | t=3s时,物体C与D间距离最大 | |
| C. | 在0~3s时间内,物体B运动的位移为5m | |
| D. | 物体A和B均做匀加速直线运动且A的速度比B的大 |
| A. | 加速度大的物体速度变化快 | B. | 加速度大的物体速度大 | ||
| C. | 加速度减少时物体速度可能增大 | D. | 加速度小的物体速度小 |
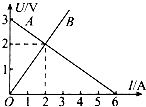 如图所示,直线A为电源的路端电压U与电流I的关系图象,直线B是电阻R的两端电压与其中电流I的关系图象,用该电源与电阻R组成闭合电路,则电源的输出功率为4W.
如图所示,直线A为电源的路端电压U与电流I的关系图象,直线B是电阻R的两端电压与其中电流I的关系图象,用该电源与电阻R组成闭合电路,则电源的输出功率为4W.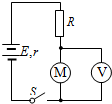 如图所示,是一提升物体用的直流电动机工作时的电路图,电动机的内阻rM=0.8Ω,电路中另一电阻R=9Ω,电源电动势E=16V,电源的内阻r=1Ω,电压表的示数U=11V.试求:
如图所示,是一提升物体用的直流电动机工作时的电路图,电动机的内阻rM=0.8Ω,电路中另一电阻R=9Ω,电源电动势E=16V,电源的内阻r=1Ω,电压表的示数U=11V.试求: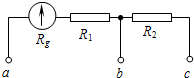 如图所示是一种电压表的原理图.电流表的内阻Rg为500Ω,满偏电流Ig为1mA.当使用a、b两个端点时,量程为0~10V,则电阻R1的阻值为9500Ω.若电阻R2的阻值为9×104Ω,则当使用a、c两个端点时,量程的最大值为100V.
如图所示是一种电压表的原理图.电流表的内阻Rg为500Ω,满偏电流Ig为1mA.当使用a、b两个端点时,量程为0~10V,则电阻R1的阻值为9500Ω.若电阻R2的阻值为9×104Ω,则当使用a、c两个端点时,量程的最大值为100V.