题目内容
宇航员测得某星球的半径为R，该星球的近地卫星（其轨道半径近似等于星球的半径R．）的周期为T．下列四个量中哪几个量可以求得？（万有引力恒量为G）（ ）
| A．该星球的质量 |
| B．近地卫星的质量 |
| C．该星球的平均密度 |
| D．该星球同步卫星的离地高度 |
A、根据G
=m
R，得星球的质量为：M=
．故A正确．
B、近地卫星是环绕天体，由上式可知质量m被约去了，故不能计算近地卫星的质量，故B错误．
C、星球的密度ρ=
=
=
．故C正确．
D、因为同步卫星的周期未知，无法求出同步卫星的轨道半径，则不能求出卫星离地的高度．故D错误．
故选：AC．
| Mm |
| R2 |
| 4π2 |
| T2 |
| 4π2R3 |
| GT2 |
B、近地卫星是环绕天体，由上式可知质量m被约去了，故不能计算近地卫星的质量，故B错误．
C、星球的密度ρ=
| M |
| V |
| ||
|
| 3π |
| GT2 |
D、因为同步卫星的周期未知，无法求出同步卫星的轨道半径，则不能求出卫星离地的高度．故D错误．
故选：AC．
练习册系列答案
相关题目
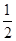。若不计其他星球的影响，该星球的第一宇宙速度是地球的第一宇宙速度的________倍，某物体在该星球表面上所受重力是在地球表面上所受重力的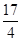__________倍。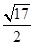
倍
倍