题目内容
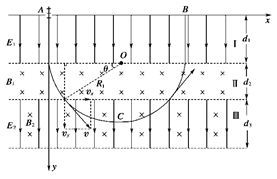
(11分)(2009·安徽省六校联考)如图所示,为某种新型设备内部电、磁场分布情况图.自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域.区域Ⅰ宽度为d1,分布有沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布有垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布有沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电荷量均不同的带正电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出.三区域都足够长,粒子的重力不计.
已知能飞回区域Ⅰ的带电粒子的质量为m=6.4×10-27kg,带电荷量为q=3.2×10-19C,且d1=10cm,d2=5cm,d3>10cm,E1=E2=40V/m,B1=4×10-3T,B2=2×10-3T.

试求:
(1)该带电粒子离开区域Ⅰ时的速度.
(2)该带电粒子离开区域Ⅱ时的速度.
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离.
已知能飞回区域Ⅰ的带电粒子的质量为m=6.4×10-27kg,带电荷量为q=3.2×10-19C,且d1=10cm,d2=5cm,d3>10cm,E1=E2=40V/m,B1=4×10-3T,B2=2×10-3T.

试求:
(1)该带电粒子离开区域Ⅰ时的速度.
(2)该带电粒子离开区域Ⅱ时的速度.
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离.
(1)2×104m/s 方向竖直向下
(2)2×104m/s 方向与x轴正向成45°角
(3)57.26cm
(2)2×104m/s 方向与x轴正向成45°角
(3)57.26cm
(1)qE1d1=mv2
得:v=2×104m/s,方向竖直向下.
(2)速度大小仍为v=2×104m/s,如图所示.
qB1v=m
方向:sinθ=
可得:θ=45°
所以带电粒子离开区域Ⅱ时的速度方向与x轴正向成45°角.
(3)设该带电粒子离开区域Ⅱ也即进入区域Ⅲ时的速度分解为vx、vy,则:vx=vy=vsin45°=×104m/s
所以:qB2vx=qB2vy=1.28×10-17N.
qE2=1.28×10-17N
qE2=qB2vx
所以带电粒子在区域Ⅲ中运动可视为沿x轴正向的速率为vx的匀速直线运动和以速率为vy,以及对应洛伦兹力qB2vy作为向心力的匀速圆周运动的叠加,轨道如图所示:
R2==10cm
T==π×10-5s
根据运动的对称性可知,带电粒子回到区域Ⅰ的上边缘的B点,距A点的距离为:d=2
代入数据可得:d≈57.26cm
得:v=2×104m/s,方向竖直向下.
(2)速度大小仍为v=2×104m/s,如图所示.
qB1v=m
方向:sinθ=
可得:θ=45°
所以带电粒子离开区域Ⅱ时的速度方向与x轴正向成45°角.
(3)设该带电粒子离开区域Ⅱ也即进入区域Ⅲ时的速度分解为vx、vy,则:vx=vy=vsin45°=×104m/s
所以:qB2vx=qB2vy=1.28×10-17N.
qE2=1.28×10-17N
qE2=qB2vx
所以带电粒子在区域Ⅲ中运动可视为沿x轴正向的速率为vx的匀速直线运动和以速率为vy,以及对应洛伦兹力qB2vy作为向心力的匀速圆周运动的叠加,轨道如图所示:

R2==10cm
T==π×10-5s
根据运动的对称性可知,带电粒子回到区域Ⅰ的上边缘的B点,距A点的距离为:d=2
代入数据可得:d≈57.26cm

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 Eq
Eq
 ,方向竖直向下。求:当小球A向下运动
,方向竖直向下。求:当小球A向下运动 时,它的加速度多大?球A在向电荷B运动的过程中,与B相距多远时速度最大?
时,它的加速度多大?球A在向电荷B运动的过程中,与B相距多远时速度最大?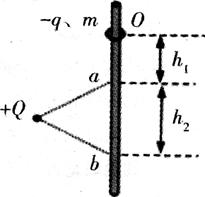

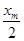 过程中,电阻R1产生的焦耳热。
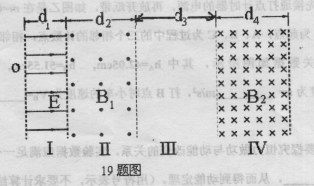
过程中,电阻R1产生的焦耳热。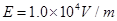 ,方向垂直边界面向右.Ⅱ、Ⅳ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为
,方向垂直边界面向右.Ⅱ、Ⅳ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为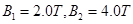 ,Ⅲ区域内无电磁场。四个区域宽度分别为
,Ⅲ区域内无电磁场。四个区域宽度分别为 .一质量
.一质量 、电荷量
、电荷量 的粒子从O点由静止释放,粒子的重力忽略不计.
的粒子从O点由静止释放,粒子的重力忽略不计. 求:
求: