题目内容
9.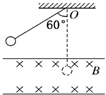 如图所示,一绝缘材料的带正电小球质量为m,电量为q,用长为L、不可伸长细线悬挂于O点,并在竖直平面内摆动,最大摆角为60°,空气阻力不计,水平磁场垂直于小球摆动的平面,当小球自左方摆到最低点时,悬线上的张力恰为零,求
如图所示,一绝缘材料的带正电小球质量为m,电量为q,用长为L、不可伸长细线悬挂于O点,并在竖直平面内摆动,最大摆角为60°,空气阻力不计,水平磁场垂直于小球摆动的平面,当小球自左方摆到最低点时,悬线上的张力恰为零,求(1)小球摆到最低点的速度为多大?
(2)小球自右方摆到最低点时悬线上的张力为多大?
分析 小球摆动过程中,受到重力、线的拉力和洛伦兹力,只有重力做功,其机械能守恒,当小球自右方摆到最低点时的速率等于自左方摆到最低点时的速率,由机械能守恒定律求出小球经过最低点时的速率.根据小球自左方摆到最低点时,悬线上的张力恰为零,由重力与洛伦兹力的合力提供向心力,由牛顿第二定律列出方程.小球自右方摆到最低点时,洛伦兹力方向向下,再由牛顿第二定律求出悬线上的张力.
解答 解:(1)因线的长度为L,小球经过最低点时速率为v.
根据机械能守恒定律得:mgL(1-cos60°)=$\frac{1}{2}$mv2,
解得:v=$\sqrt{gL}$
(2)当小球自左方摆到最低点时,有:qvB-mg=m$\frac{{v}^{2}}{L}$①
当小球自右方摆到最低点时,有:F-mg-qvB=m$\frac{{v}^{2}}{L}$②
由①+②得:F=2mg+2m$\frac{{v}^{2}}{L}$=4mg.
答:(1)小球摆到最低点的速度为$\sqrt{gL}$;
(2)小球自右方摆到最低点时悬线上的张力为4mg.
点评 本题磁场中的力学问题,考查综合应用机械能守恒定律和牛顿第二定律解题的能力,抓住洛伦兹力不做功的特点.

练习册系列答案
相关题目
19. 如图所示,单匝矩形线圈abcd在外力作用下,先后两次向右匀速进入同一匀强磁场,已知两次进入磁场的过程中,线圈中电流之比为2:1,则两次相比较( )
如图所示,单匝矩形线圈abcd在外力作用下,先后两次向右匀速进入同一匀强磁场,已知两次进入磁场的过程中,线圈中电流之比为2:1,则两次相比较( )
 如图所示,单匝矩形线圈abcd在外力作用下,先后两次向右匀速进入同一匀强磁场,已知两次进入磁场的过程中,线圈中电流之比为2:1,则两次相比较( )
如图所示,单匝矩形线圈abcd在外力作用下,先后两次向右匀速进入同一匀强磁场,已知两次进入磁场的过程中,线圈中电流之比为2:1,则两次相比较( )| A. | 第一次与第二次线圈的速度之比为2:1 | |
| B. | 第一次与第二次外力做功的功率之比为4:1 | |
| C. | 第一次全部进入磁场和第二次全部进入磁场线圈中产生的热量之比为8:1 | |
| D. | 第一次全部进入磁场和第二次全部进入磁场,通过线圈中同一横截面的电荷量之比为2:1 |
20. 如图所示,在沿x轴正向的匀强电场E中,有一动点A以O为圆心,r为半径做逆时针转动,当OA与x轴正向成θ角时O、A两点间的电势差为( )
如图所示,在沿x轴正向的匀强电场E中,有一动点A以O为圆心,r为半径做逆时针转动,当OA与x轴正向成θ角时O、A两点间的电势差为( )
 如图所示,在沿x轴正向的匀强电场E中,有一动点A以O为圆心,r为半径做逆时针转动,当OA与x轴正向成θ角时O、A两点间的电势差为( )
如图所示,在沿x轴正向的匀强电场E中,有一动点A以O为圆心,r为半径做逆时针转动,当OA与x轴正向成θ角时O、A两点间的电势差为( )| A. | UOA=E•r | B. | UOA=E•r sinθ | C. | UOA=E•r sinθ | D. | UOA=-E•r cosθ |
14.土卫十和土卫十一是土星的两颗卫星,都沿近似为圆周的轨道绕土星运动.其参数如表:
两卫星相比,土卫十( )
| 卫星半径(m) | 卫星质量(kg) | 轨道半径(m) | |
| 土卫十 | 8.90×104 | 2.01×1018 | 1.51×1018 |
| 土卫十一 | 5.70×104 | 5.60×1017 | 1.51×1018 |
| A. | 受土星的万有引力较大 | |
| B. | 绕土星的圆周运动的周期较大 | |
| C. | 绕土星做圆周运动的向心加速度较大 | |
| D. | 动能较大 |
1. 如图所示,在光滑水平面上放置一个质量为M的滑块,滑块的一侧是一个$\frac{1}{4}$圆弧OEF,圆弧半径为R,E点切线水平,另有一个质量为m的小球以速度v0从A点冲上滑块,不计摩擦,下列说法中正确的是( )
如图所示,在光滑水平面上放置一个质量为M的滑块,滑块的一侧是一个$\frac{1}{4}$圆弧OEF,圆弧半径为R,E点切线水平,另有一个质量为m的小球以速度v0从A点冲上滑块,不计摩擦,下列说法中正确的是( )
 如图所示,在光滑水平面上放置一个质量为M的滑块,滑块的一侧是一个$\frac{1}{4}$圆弧OEF,圆弧半径为R,E点切线水平,另有一个质量为m的小球以速度v0从A点冲上滑块,不计摩擦,下列说法中正确的是( )
如图所示,在光滑水平面上放置一个质量为M的滑块,滑块的一侧是一个$\frac{1}{4}$圆弧OEF,圆弧半径为R,E点切线水平,另有一个质量为m的小球以速度v0从A点冲上滑块,不计摩擦,下列说法中正确的是( )| A. | 当v0=$\sqrt{2gR}$时,小球能到达F点 | |
| B. | 若小球的速度足够大,球将从滑块的右侧离开滑块 | |
| C. | 小球在圆弧上运动的过程中,滑块的动能增大,小球的机械能减小 | |
| D. | 若滑块固定,小球返回E点时对滑块的压力为mg+m$\frac{{{v}_{0}}^{2}}{R}$ |
18.一氢气球升高到离地面80m的高空时从上面掉落下一物体,物体又上升了10m后开始下落.若取向上为正,以物体刚开始掉落时的位置为坐标原点,则物体上升到最高点的位置坐标和物体落到底面上时的位置坐标分别为( )
| A. | 90m,0 | B. | 10m,-80m | C. | 10m,0 | D. | 90m,-80m |

 交流发电机模型的矩形线圈abcd在匀强磁场中,绕OO′轴匀速转动,线圈共有n匝,线圈面积S,线圈内阻为r,外电路电阻为R,磁感应强度是B,线圈转动的角速度是ω,如图所示,求:
交流发电机模型的矩形线圈abcd在匀强磁场中,绕OO′轴匀速转动,线圈共有n匝,线圈面积S,线圈内阻为r,外电路电阻为R,磁感应强度是B,线圈转动的角速度是ω,如图所示,求: