题目内容
 如图所示,光滑圆柱半径为R,被固定在水平平台上,用轻绳跨过圆柱体与两小球m1、m2相连(m1、m2分别为它们的质量),开始时让m1放在平台上,两边绳绷直,两球从静止开始m1上升,m2下降.当m1上升到圆柱的最高点时,球m1对轨道的压力0.2m1g,求:
如图所示,光滑圆柱半径为R,被固定在水平平台上,用轻绳跨过圆柱体与两小球m1、m2相连(m1、m2分别为它们的质量),开始时让m1放在平台上,两边绳绷直,两球从静止开始m1上升,m2下降.当m1上升到圆柱的最高点时,球m1对轨道的压力0.2m1g,求:(1)小球m1上升到圆柱的最高点时,速度多大?(用g、R表示)
(2)两球从静止开始至m1上升到圆柱的最高点,系统减少的势能为多少?
(3)m2应为m1的多少倍?
分析:(1)小球m1上升到圆柱的最高点时,对轨道的压力0.2m1g,重力和支持力的合力提供向心力,根据牛顿第二定律列式求解速度;
(2)两球从静止开始至m1上升到圆柱的最高点过程,根据Ep=mgh求解两个球重力势能的减小量;
(3)两个球组成的系统机械能守恒,根据守恒定律列式求解两球的质量关系.
(2)两球从静止开始至m1上升到圆柱的最高点过程,根据Ep=mgh求解两个球重力势能的减小量;
(3)两个球组成的系统机械能守恒,根据守恒定律列式求解两球的质量关系.
解答:解:(1)当m1上升到圆柱的最高点时,物体受重力和支持力的合力提供向心力,支持力与压力是相互作用力,等大、反向、共线,故根据牛顿第二定律有:
F向=m1g-0.2m1g=m1
解得:v=
(2)两球从静止开始至m1上升到圆柱的最高点,m1与m2组成的系统减少的势能为:
△EP减=m2g(R+
)-m1g?2R
(3)根据系统机械能守恒,有:
△EP减=△Ek增
故有:m2g(R+
)-m1g2R=
m1v2+
m2v2
解得:m2=
m1
答:(1)小球m1上升到圆柱的最高点时,速度为
;
(2)两球从静止开始至m1上升到圆柱的最高点,系统减少的势能为m2g(R+
)-m1g2R;
(3)m2应为m1的
倍.
F向=m1g-0.2m1g=m1
| v2 |
| R |
解得:v=
| 0.8gR |
(2)两球从静止开始至m1上升到圆柱的最高点,m1与m2组成的系统减少的势能为:
△EP减=m2g(R+
| 2πR |
| 4 |
(3)根据系统机械能守恒,有:
△EP减=△Ek增
故有:m2g(R+
| 2πR |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:m2=
| 24 |
| 6+5π |
答:(1)小球m1上升到圆柱的最高点时,速度为
| 0.8gR |
(2)两球从静止开始至m1上升到圆柱的最高点,系统减少的势能为m2g(R+
| 2πR |
| 4 |
(3)m2应为m1的
| 24 |
| 6+5π |
点评:本题第一问关键明确重力和支持力的合力提供向心力;第二问和第三问关键明确两个小球的系统机械能守恒,根据机械能守恒定律列式求解即可.

练习册系列答案
相关题目
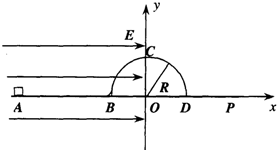 如图所示,光滑水平面上固定着一半径为R的光滑半圆柱体,半圆柱体的轴线过坐标原点O,在x<0 一侧的整个空间存在电场强度大小为E、方向水平向右的匀强电场一个质量为m、带正电荷q的小滑块,从水平面上的A点由静止释放,到达B点后沿半圆柱面继续上滑(B点处有一光滑小圆弧面连接水平面与半圆柱面),达到半圆柱面顶点C时,小滑块对半圆柱面的压力恰好为零,离开柱面后小滑块落到水平上的P点.试求:
如图所示,光滑水平面上固定着一半径为R的光滑半圆柱体,半圆柱体的轴线过坐标原点O,在x<0 一侧的整个空间存在电场强度大小为E、方向水平向右的匀强电场一个质量为m、带正电荷q的小滑块,从水平面上的A点由静止释放,到达B点后沿半圆柱面继续上滑(B点处有一光滑小圆弧面连接水平面与半圆柱面),达到半圆柱面顶点C时,小滑块对半圆柱面的压力恰好为零,离开柱面后小滑块落到水平上的P点.试求: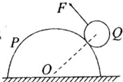 如图所示,半圆柱体P放在粗糙的水平面上,一个光滑均匀的小圆柱体Q,受到一个始终与两圆心连线垂直的力F作用,在F的作用下缓慢地由最低端移到半圆柱的顶端的过程中,下列说法中正确的是( )
如图所示,半圆柱体P放在粗糙的水平面上,一个光滑均匀的小圆柱体Q,受到一个始终与两圆心连线垂直的力F作用,在F的作用下缓慢地由最低端移到半圆柱的顶端的过程中,下列说法中正确的是( )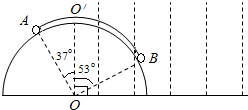 (2012?盐城二模)如图所示,半径为1m的半圆柱体固定在水平面上,小球A和B通过轻绳相连,静止在光滑的圆柱面上,与竖直方向的夹角分别为37°和53°.OO’右侧有一特殊区域,可以对A球施加竖直恒力作用,而对B没有力的作用.某时刻小球受到干扰失去平衡,从静止开始运动,A沿圆柱面向上,B沿圆柱面向下,当A球刚进入特殊区域时剪断轻绳,恰能离开圆柱面落到水平面上.已知A球的质量为1Kg,sin37°=0.6,cossin37°=0.8,重力加速度g=10m/s2.求
(2012?盐城二模)如图所示,半径为1m的半圆柱体固定在水平面上,小球A和B通过轻绳相连,静止在光滑的圆柱面上,与竖直方向的夹角分别为37°和53°.OO’右侧有一特殊区域,可以对A球施加竖直恒力作用,而对B没有力的作用.某时刻小球受到干扰失去平衡,从静止开始运动,A沿圆柱面向上,B沿圆柱面向下,当A球刚进入特殊区域时剪断轻绳,恰能离开圆柱面落到水平面上.已知A球的质量为1Kg,sin37°=0.6,cossin37°=0.8,重力加速度g=10m/s2.求 ,方向沿水平方向,若小球在水平面上的落点为C(图中未画出),则
,方向沿水平方向,若小球在水平面上的落点为C(图中未画出),则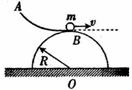
 R
R