题目内容
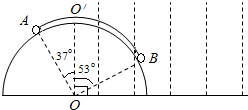 (2012?盐城二模)如图所示,半径为1m的半圆柱体固定在水平面上,小球A和B通过轻绳相连,静止在光滑的圆柱面上,与竖直方向的夹角分别为37°和53°.OO’右侧有一特殊区域,可以对A球施加竖直恒力作用,而对B没有力的作用.某时刻小球受到干扰失去平衡,从静止开始运动,A沿圆柱面向上,B沿圆柱面向下,当A球刚进入特殊区域时剪断轻绳,恰能离开圆柱面落到水平面上.已知A球的质量为1Kg,sin37°=0.6,cossin37°=0.8,重力加速度g=10m/s2.求
(2012?盐城二模)如图所示,半径为1m的半圆柱体固定在水平面上,小球A和B通过轻绳相连,静止在光滑的圆柱面上,与竖直方向的夹角分别为37°和53°.OO’右侧有一特殊区域,可以对A球施加竖直恒力作用,而对B没有力的作用.某时刻小球受到干扰失去平衡,从静止开始运动,A沿圆柱面向上,B沿圆柱面向下,当A球刚进入特殊区域时剪断轻绳,恰能离开圆柱面落到水平面上.已知A球的质量为1Kg,sin37°=0.6,cossin37°=0.8,重力加速度g=10m/s2.求(1)B球质量
(2)A球进入特殊区域前瞬间圆柱体对它的支持力
(3)A球落地点与O点的距离.
分析:(1)小球A和B通过轻绳相连,静止在光滑的圆柱面上,根据平衡条件即可求得B的质量;
(2)先根据AB系统机械能守恒,求出A球到达O′时的速度,在O′点根据向心力公式即可求得A球进入特殊区域前瞬间圆柱体对它的支持力;
(3)A球离开圆柱面后做类平抛运动,根据平抛运动基本公式即可求解.
(2)先根据AB系统机械能守恒,求出A球到达O′时的速度,在O′点根据向心力公式即可求得A球进入特殊区域前瞬间圆柱体对它的支持力;
(3)A球离开圆柱面后做类平抛运动,根据平抛运动基本公式即可求解.
解答:解:(1)根据平衡条件有:
mAgsin37°=mBgsin53°
所以mB=
mA=0.75kg
(2)AB系统机械能守恒,则有:
mBgsin37°-mAgR(1-cos37°)=
(mA+mB)v2
解得:v=
m/s
A球在最高点有:
mg-FN=m
解得:FN=
N
(3)A球做类平抛运动,则有g′=
=
m/s2
水平方向有:x=vt
竖直方向有:R=
g′t2
解得x=
m
答:(1)B球质量为0.75kg;
(2)A球进入特殊区域前瞬间圆柱体对它的支持力为
N;
(3)A球落地点与O点的距离为
m.
mAgsin37°=mBgsin53°
所以mB=
| 3 |
| 4 |
(2)AB系统机械能守恒,则有:
mBgsin37°-mAgR(1-cos37°)=
| 1 |
| 2 |
解得:v=
|
A球在最高点有:
mg-FN=m
| v2 |
| R |
解得:FN=
| 50 |
| 7 |
(3)A球做类平抛运动,则有g′=
| mAg-FN |
| mA |
| 20 |
| 7 |
水平方向有:x=vt
竖直方向有:R=
| 1 |
| 2 |
解得x=
| 2 |
答:(1)B球质量为0.75kg;
(2)A球进入特殊区域前瞬间圆柱体对它的支持力为
| 50 |
| 7 |
(3)A球落地点与O点的距离为
| 2 |
点评:本题主要考查了机械能守恒定律、向心力公式、平抛运动基本公式的直接应用,要求同学们能正确对小球进行受力分析,难度适中.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 (2012?盐城二模)两根相距为L的平行光滑金属导轨竖直放置,上端通过导线连接阻值为R的电阻.现有n个条形匀强磁场,方向与导轨平面垂直,磁场区域的宽度为a,间距也为a.一个质量为m、长为L的导体棒(电阻不计)与导轨垂直,在距磁场区域1为a的位置由静止开始释放,此后一直没有离开导轨,且每当进入磁场区域均做匀速运动.求
(2012?盐城二模)两根相距为L的平行光滑金属导轨竖直放置,上端通过导线连接阻值为R的电阻.现有n个条形匀强磁场,方向与导轨平面垂直,磁场区域的宽度为a,间距也为a.一个质量为m、长为L的导体棒(电阻不计)与导轨垂直,在距磁场区域1为a的位置由静止开始释放,此后一直没有离开导轨,且每当进入磁场区域均做匀速运动.求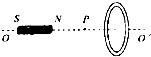 (2012?盐城二模)超导体的电阻为零,如果闭合的超导电路内有电流,这个电流不产生焦耳热,所以不会自行消失.有一超导圆环于图示位置,此时圆环中没有电流.将一根条形磁体沿圆环的中心轴OO’移到P点.以下说法正确的是( )
(2012?盐城二模)超导体的电阻为零,如果闭合的超导电路内有电流,这个电流不产生焦耳热,所以不会自行消失.有一超导圆环于图示位置,此时圆环中没有电流.将一根条形磁体沿圆环的中心轴OO’移到P点.以下说法正确的是( ) (2012?盐城二模)如图所示,A、B两物体静止在粗糙水平面上,其间用一根轻弹簧相连,弹簧的长度大于原长.若再用一个从零开始缓慢增大的水平力F向右拉物体B,直到A即将移动,此过程中,地面对B的摩擦力f1和对A的摩擦力f2的变化情况( )
(2012?盐城二模)如图所示,A、B两物体静止在粗糙水平面上,其间用一根轻弹簧相连,弹簧的长度大于原长.若再用一个从零开始缓慢增大的水平力F向右拉物体B,直到A即将移动,此过程中,地面对B的摩擦力f1和对A的摩擦力f2的变化情况( )