题目内容
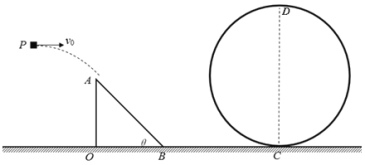
【题目】如图所示,AB是倾角θ=45°的倾斜轨道,BC是一个水平轨道(物体经过B处时无机械能损失),AO是一竖直线,O、B、C在同一水平面上,竖直平面内的光滑圆形轨道最低点与水平面相切与C点,已知A、O两点间的距离h=1m,B、C两点间的距离d=2.0m,圆形轨道的半径R=1m。一质量m=2kg的小物体,从与O点水平距离x0=3.6m的P点水平抛出,恰好从A点以平行斜面的速度进入倾斜轨道,最后进入圆形轨道。小物件与倾斜轨道AB、水平轨道BC之问的动摩擦因数都是μ=0.5,g取10m/s2)。
(1)求小物体从P点抛出时的速度v0和P点的高度H;
(2)求小物体运动到圆形轨道最高点D时,对圆形轨道的压力;
(3) 若小物体从Q点水平抛出,恰好从A点以平行斜面的速度进入倾斜轨道,最后进入圆形轨道,且小物体不能脱离轨道,求Q、O两点的水平距离x的取值范围。
【答案】(1)6m/s,2.8m;(2)N=24N;(3)0.5m<x≤15m或x≥3m
【解析】
(1)小物体从P到A做平抛运动,由题知,物体经过A点时速度平行于斜面向下,设物体经过A点时竖直分速度大小为vy,如图所示

则有
vy=v0tan45°=v0,![]()
又
![]()
可得
![]() ,
,![]()
水平距离
![]()
联立解得
v0=6m/s,H=2.8m
(2)物体从P到D的过程,由动能定理得:
![]()
在D点,由牛顿第二定律得
![]()
联立解得
N=24N
由牛顿第三定律知,物体对圆形轨道的压力大小为24N。
(3)要保证小物体不脱离轨道,可分两种情况进行讨论:第一种情况,能通过最高点D,第二种情况,所能到达的最高点小于等于圆心的高度。
第一种情况,小球能通过最高点D时,设O、Q的水平距离为x1,恰好通过圆形轨道的最高点D。小物体从Q点水平抛出后,恰好从A点以平行于斜面的速度进入倾斜轨道时,根据第1问可得小物体到达A点的速度
![]()
恰好通过圆形轨道的最高点D时,只有重力充当向心力,得
![]()
由动能定理得
![]()
代入数据解得
x1=3m
小物体能通过最高点D,所以O、Q的水平距离
x≥x1=3m
第二种情况,所能到达的高度小于等于圆心的高度时,设O、Q的水平距离为x2,恰好到达圆心高度。小物体从Q点水平抛出后,恰好从A点以平行于斜面的速度进入倾斜轨道时,根据第1问可得小物体到达A点的速度
![]()
恰好到达圆心的高度时,末速度为0,由动能定理得
![]()
代入数据解得
x2=1.5m
设O、Q的水平距离为x3时,恰好到达圆形轨道处,小物体从Q点水平抛出后,恰好从A以平行于斜面的速度进入倾斜轨道时,根据第1问可得小物体到达A点的速度
![]()
恰好到达圆形轨道时,到C点的速度为0。由动能定理得
![]()
代入数据解得
x3=0.5m
小物体能进入圆形轨道,不脱离,O、Q的水平距离应满足:
0.5m<x≤1.5m
综上所述,若小物体从Q点水平抛出,恰好从A点以平行斜面的速度进入倾斜轨道,最后进入圆形轨道,且小物体不能脱离轨道,Q、O两点的水平距离x的取值范围为
0.5m<x≤1.5m或x≥3m