题目内容
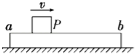
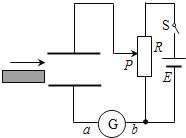
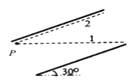
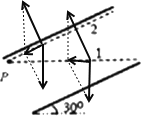
【题目】如图所示,板长为L的平行板电容器与一直流电源相连接,其极板与水平面成300角;若粒子甲乙以相同的大小的初速度![]() 由图中的P点射入电容器,分别沿着虚线1和2运动,然后离开电容器;虚线1为连接上下极板边缘的水平线,虚线2为平行且靠近上极板的直线,则下列关于两粒子的说法正确的是( )
由图中的P点射入电容器,分别沿着虚线1和2运动,然后离开电容器;虚线1为连接上下极板边缘的水平线,虚线2为平行且靠近上极板的直线,则下列关于两粒子的说法正确的是( )
A. 两者均做匀速直线运动
B. 两者电势能均逐渐增加
C. 两者的比荷之比为![]()
D. 两者离开电容器时的速率之比为![]()
【答案】D
【解析】
根据题意可知,粒子做直线运动,则电场力与重力的合力与速度在同一直线上,所以电场力只能垂直极板向上,受力如图所示;根据受力图,粒子做直线运动,则电场力与重力的合力与速度方向反向,粒子做匀减速直线运动,故A错误;
粒子甲受到的电场力与位移方向的夹角为钝角,所以电场力做负功,电势能逐渐增加;粒子乙运动的方向与电场力的方向垂直,电场力不做功,所以粒子的电势能不变。故B错误;根据受力图,对甲:m甲g=q甲Ecos30°=![]() q甲E,所以:
q甲E,所以:![]()
对乙:m乙gcos30°=q乙E,所以:![]() ;所以:
;所以:![]() ,故C错误;带电微粒甲沿水平直线运动,合力做的功:W1=m甲gtan30°
,故C错误;带电微粒甲沿水平直线运动,合力做的功:W1=m甲gtan30°![]() =
=![]() m甲gL,根据动能定理得:
m甲gL,根据动能定理得:![]() ;所以:
;所以:![]() ;带电微粒乙沿平行于极板的直线运动,合力做的功:W2=m乙gsin30°L=
;带电微粒乙沿平行于极板的直线运动,合力做的功:W2=m乙gsin30°L=![]() m乙gL,根据动能定理得:
m乙gL,根据动能定理得:![]() ,所以:v乙=
,所以:v乙=![]() ;所以:
;所以:![]() .故D正确。故选D。
.故D正确。故选D。

练习册系列答案
相关题目