��Ŀ����
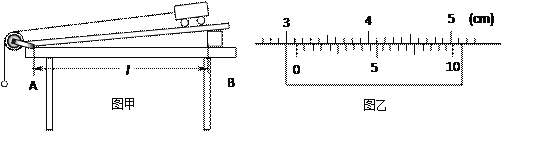
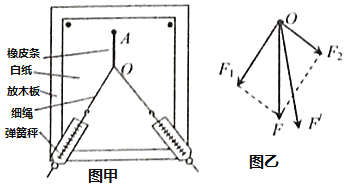
����Ŀ����ͼ��ʾ�������Ϊ30���б���Ϲ̶�һ���費�ƵĹ⻬ƽ�н������죬����ΪL���¶˽�����ֵΪR�ĵ��裬���촦����ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB��������б�洹ֱ��ͼ��δ������������Ϊm������ΪL����ֵ��СҲΪR�Ľ�����ab��̶���б���Ϸ��ľ���ϵ��Ϊk�ľ�Ե������ӣ����ɴ���ԭ�������������ֽ��������ͬʱʹ�����������б�����µ��ٶ�![]() ���ӿ�ʼ�˶���ֹͣ�˶��Ĺ����н�����ʼ���뵼�촹ֱ���������ýӴ�������ʼ���ڵ������ڣ��������ٶ�Ϊg��������������
���ӿ�ʼ�˶���ֹͣ�˶��Ĺ����н�����ʼ���뵼�촹ֱ���������ýӴ�������ʼ���ڵ������ڣ��������ٶ�Ϊg��������������
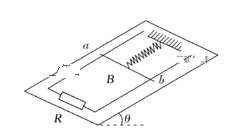
A.��ʼ�˶�ʱ�������뵼��Ӵ�����ѹΪ![]()
B.ͨ������R��������һ����![]()
C.ͨ������R���ܵ����Ϊ![]()
D.��·����������������![]()
���𰸡�C
��������
A. ��ʼʱ�������и�Ÿ��߲����ĸ�Ӧ�綯�ƣ�E=BLv0���������뵼��Ӵ����ĵ�ѹ��
![]()
��A����
B. ��������ʼ�����˶�ʱ�����������˶��������������ٶ����ʱ��Ӧ�����������������ٶȴ���v0�����������ڣ�![]() ����B����
����B����
C. ���ս�������ֹ����ʱ����ƽ�������ã�
mgsin30��=kx
��ʱ���ɵ��쳤����
![]()
ͨ��R���ܵ������
![]()
��C��ȷ��
D. �������غ㶨�ɵã�
![]()
��ã�
![]()
��D����

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ