题目内容
13. 图示为一列沿x轴负方向传播的机械波,实线和虚线分别为t时刻和t+△t时刻的波形,B和C是横坐标分别为d和3d的两个质点.则t时刻质点B的振动方向为y轴正方向,该波的波速为$\frac{(6k+5)d}{2△t}$,(其中k=0,1,2,3…).
图示为一列沿x轴负方向传播的机械波,实线和虚线分别为t时刻和t+△t时刻的波形,B和C是横坐标分别为d和3d的两个质点.则t时刻质点B的振动方向为y轴正方向,该波的波速为$\frac{(6k+5)d}{2△t}$,(其中k=0,1,2,3…).
分析 已知波的传播方向,运用波形平移法分析质点的振动方向.根据波的周期性,写出波传播距离的通项,再求解波速的通项.
解答 解:波沿x轴负方向传播,运用波形平移法分析知,t时刻质点B的振动方向为y轴正方向.
由图知,该波的波长为 λ=3d
根据波的周期性,可知波在△t时间传播的距离为△x=kλ+$\frac{5}{2}$d=3kd+$\frac{5}{2}d$,(其中k=0,1,2,3…).
则波速为 v=$\frac{△x}{△t}$=$\frac{(6k+5)d}{2△t}$,(其中k=0,1,2,3…).
故答案为:y轴正方向,$\frac{(6k+5)d}{2△t}$,(其中k=0,1,2,3…).
点评 本题是多解问题,关键要理解波的周期性及重复性,是会通过波形微平移法得到波的传播距离的通项,最后求解传播速度通项.

练习册系列答案
相关题目
3.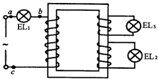 如图,一个理想变压器上有三组线圈,三组线圈匝数之比为n1:n2:n3=3:2:1,现将三只相同的灯泡分别接入三组线圈中,并把n1的接线端接上交变电源,接通电源后,下列各项正确的是( )
如图,一个理想变压器上有三组线圈,三组线圈匝数之比为n1:n2:n3=3:2:1,现将三只相同的灯泡分别接入三组线圈中,并把n1的接线端接上交变电源,接通电源后,下列各项正确的是( )
 如图,一个理想变压器上有三组线圈,三组线圈匝数之比为n1:n2:n3=3:2:1,现将三只相同的灯泡分别接入三组线圈中,并把n1的接线端接上交变电源,接通电源后,下列各项正确的是( )
如图,一个理想变压器上有三组线圈,三组线圈匝数之比为n1:n2:n3=3:2:1,现将三只相同的灯泡分别接入三组线圈中,并把n1的接线端接上交变电源,接通电源后,下列各项正确的是( )| A. | 若EL1正常发光,那么EL2、EL3都不能正常发光 | |
| B. | 若EL2正常发光,那么EL1将烧毁 | |
| C. | 若EL2正常发光,那么EL1、EL3都不能到正常亮度 | |
| D. | 若EL3正常发光,那么EL2将烧毁 |
4.如图所示,光滑轨道右端固定一个竖直挡板,挡板左边连接一轻质弹簧,小球以初速度v0经过轨道的a、b、c、d、e后压缩弹簧直至f点,不考虑空气阻力,则下列说法正确的是( )


| A. | 小球从c到d过程重力做负功 | |
| B. | 在f点弹簧的弹性势能最大 | |
| C. | 小球在d点机械能大于在b点的机械能 | |
| D. | 小球在从a点运动到f点全过程中机械能守恒 |
1.如图所示,A、B是某“门”电路的输入信号,Z是相应的输出信号.由此可以判断,该门电路是( )


| A. | “或”门 | B. | “与”门 | C. | “非”门 | D. | “与非”门 |
8.下列说法中,正确的是( )
| A. | 只有热传递才可以改变物体的内能 | |
| B. | 气体温度越高,每个分子运动的速率一定越大 | |
| C. | 布朗运动是指在显微镜下观察到的液体分子的无规则运动 | |
| D. | 热量不可能由低温物体传给高温物体而不发生其他变化 |
18. 如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )
如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )
 如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )
如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )| A. | 有顺时针方向的电流且有收缩的趋势 | |
| B. | 有顺时针方向的电流且有扩张的趋势 | |
| C. | 有逆时针方向的电流且有收缩的趋势 | |
| D. | 有逆时针方向的电流且有扩张的趋势 |
5.物理学家通过对α粒子散射实验结果的分析( )
| A. | 提出了原子的葡萄干蛋糕模型 | |
| B. | 确认在原子内部存在α粒子 | |
| C. | 认定α粒子发生大角度散射是受到电子的作用 | |
| D. | 认识到原子的全部正电荷和几乎全部的质量都集中在一个很小的核内 |
 如图所示,一个左右都与汞气相通的固定直筒水平放置,内部横截面积为S=0.01m2.中间用两个活塞A和B封住一定质量的理想气体.A、B都可以沿圆筒无摩擦地左右滑动,但不漏气.A的质量可以不计,B的质量为M,并与一个劲度系数为5×103N/m的较大的弹簧相连.已知大气压P0=1×105Pa,平衡时,两个活塞间的距离L0=0.6m,现在保持温度不变,用水平外力使活塞A向右缓慢移动0.14m,求这个外力的大小.
如图所示,一个左右都与汞气相通的固定直筒水平放置,内部横截面积为S=0.01m2.中间用两个活塞A和B封住一定质量的理想气体.A、B都可以沿圆筒无摩擦地左右滑动,但不漏气.A的质量可以不计,B的质量为M,并与一个劲度系数为5×103N/m的较大的弹簧相连.已知大气压P0=1×105Pa,平衡时,两个活塞间的距离L0=0.6m,现在保持温度不变,用水平外力使活塞A向右缓慢移动0.14m,求这个外力的大小.