题目内容
15.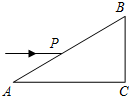 如图所示,三棱镜的横截面为直角三角形ABC,∠A=30°,∠B=60°,一束平行于AC的光线自AB边的P点射入三棱镜,若棱镜的折射率n=$\sqrt{3}$,光在真空中的速度为c.
如图所示,三棱镜的横截面为直角三角形ABC,∠A=30°,∠B=60°,一束平行于AC的光线自AB边的P点射入三棱镜,若棱镜的折射率n=$\sqrt{3}$,光在真空中的速度为c.①求光在棱镜中的传播速度;
②通过计算说明光线射出棱镜时的出射方向.
分析 根据入射角和折射角大小关系,作出光路图.根据几何关系求出光线在P点的入射角和折射角,根据折射定律求出折射率的大小.
解答 解:①根据光在介质中的传播速度公式v=$\frac{c}{n}$,可得:v=$\frac{c}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}c$.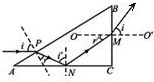
根据几何关系知,关系在AB面上的入射角为:i=60°,
根据折射定律,可求得折射角r=30°
在AC边上入射角等于60°,则sin60°=$\frac{\sqrt{3}}{2}$>$\frac{1}{n}$;
所以在AC边上发生全反射.
根据几何关系可得,在BC边上入射角等于30°,再由折射定律,可求出折射角等于60°,
所以出射光线与CB的夹角为30°,斜向上,光路图如图所示.
答:①光在棱镜中的传播速度$\frac{\sqrt{3}}{3}c$;
②光线射出棱镜时的出射方向如图所示.
点评 本题考查光的折射问题,对数学几何能力的要求较高,平时需加强训练,提高解题能力,同时掌握光的折射定律,注意正确的作图是解题的关键.

练习册系列答案
相关题目
5.某质点由A到B点到C点做匀加速直线运动,前2s和后2s位移分别为AB=8m和BC=12m.该质点的加速度及经B点的瞬时速度分别是( )
| A. | 1 m/s2,5 m/s | B. | 2 m/s2,5 m/s | C. | 1 m/s2,10 m/s | D. | 2 m/s2,10 m/s |
3.甲、乙两物体同时从一点向同一方向做直线运动,各自速度随时间变化的情况如图所示,由图可知( )
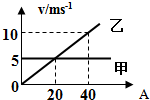

| A. | 甲做匀速直线运动,乙做初速度为0的匀加速直线运动 | |
| B. | 开始时甲比乙快,20s后乙比甲快 | |
| C. | 40s末甲、乙两物体相遇 | |
| D. | 20s末甲、乙两物体相遇 |
10.关于向心力,下列说法正确的是( )
| A. | 向心力是按其效果来命名的,做匀速圆周运动的物体需要外界提供一个向心力,谁来提供这个向心力,可以是某一个力(如摩擦力、弹力等),也可以是某几个力的合力,它并不是做匀速圆周运动的物体另受到的一种新的性质力 | |
| B. | 向心力的特点是与速度垂直,它不改变速度的大小,只改变速度的方向,它是产生向心加速度的原因 | |
| C. | 向心力是变力,它的方向总是指向圆心,物体在圆周上不同位置向心力指向不同,因此,它的方向是时刻在变化 | |
| D. | 在匀速圆周运动中向心力是恒量 |
20.光滑绝缘水平面上,B、C、D四等分线段AE,M、N是两个完全一样的小球,带有等量同种电荷,C处固定一竖直绝缘挡板,若小球N放在D处,将小球M放在C处,同时由静止释放两球,小球N到达E处的速度大小为v;若移去挡板,小球N仍放在D处,而将小球M放在B处,同时由静止释放两球,小球N到达E处的速度大小为v′,则v′与v大小之比是( )
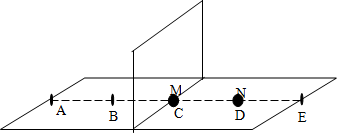

| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
4.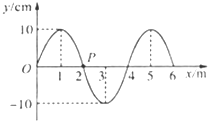 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )| A. | 周期为4.0 s,振幅为20 cm | |
| B. | 经过半周期的时间,P质点运动到水平坐标4m的位置 | |
| C. | 传播方向沿x轴正向 | |
| D. | 传播速度为10 m/s | |
| E. | 经过0.6s,P点经过的路程为60cm,且向下运动 |
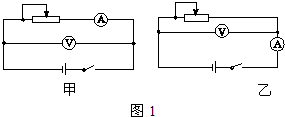

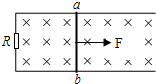 如图所示,匀强磁场磁感应强度为B=0.8T,方向垂直轨道平面,导轨间距L=0.5m,拉力F=0.2N,电阻R=4Ω,导体ab的质量m=0.1kg,杆的电阻可忽略;一切摩擦不计.求:
如图所示,匀强磁场磁感应强度为B=0.8T,方向垂直轨道平面,导轨间距L=0.5m,拉力F=0.2N,电阻R=4Ω,导体ab的质量m=0.1kg,杆的电阻可忽略;一切摩擦不计.求: