Question

如图所示，两根质量均为m=2kg的金属棒垂直地放在光滑的水平导轨上，左右两部分导轨间距之比为1∶2，导轨间有大小相等但左右两部分方向相反的匀强磁场，CD棒电阻为AB棒电阻的两倍，不计导轨电阻，今用250N的水平力F向右拉CD棒，在CD棒运动0.5m的过程中，两棒上产生的焦耳热共为45J，此时CD棒速率为8m/s，立即撤去拉力F，设导轨足够长且两棒始终在不同磁场中运动，求：
（1）撤去拉力F瞬间AB棒速度v_A；
（2）两棒最终匀速运动的速度v_A′和v_C′。

Answer 1

解：（1）撤去拉力F瞬间，由能量守恒定律得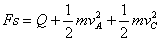： 代入数据解得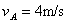： AB棒速度v_A方向向左 （2）撤去拉力F后，AB棒继续向左加速运动，而CD棒向右开始减速运动，两棒最终匀速运动时，电路中电流为零（整个回路磁通量保持不变），两棒切割磁感应电动势大小相等。即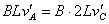： 得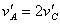： 对两棒分别应用动量定理，有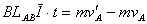 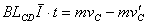因L_CD=2L_AB 故有 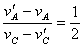联立以上各式解得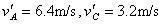： v_A′方向向左，v_C′方向向右。