题目内容
（12分）如图所示，两根质量均为m、电阻均为R、长度均为l的导体棒a、b，用两条等长的、质量和电阻均可忽略的、不可伸长的柔软长直导线连接后，b放在距地面足够高的光滑绝缘水平桌面上，a靠在桌子的光滑绝缘侧面上；两根导体棒均与桌子边缘平行。整个空间存在水平向右的匀强磁场，磁感应强度为B。开始时两棒静止，自由释放后开始运动，导体棒a在落地前就已匀速运动，此时导体棒b仍未离开桌面。已知两条导线除桌边拐弯处外其余部位均处于伸直状态，导线与桌子侧棱间无摩擦。
（1）试求导体棒匀速运动时的速度大小。
（2）从自由释放到刚匀速运动的过程中，若通过导体棒横截面的电荷量为q，求该过程中系统产生的焦耳热。
【答案】
(1) 
(2) 
【解析】
试题分析：（1）设导体棒匀速运动时的速度为v，导体棒a切割磁感线产生的电动势为E，则：
对a棒：E=Blv 1分
F安=BIl 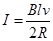1分
1分
mg=F安 1分
联立解得：
1分
（2）从自由释放到刚匀速运动的过程中，设a棒下降的高度为h，则：
回路中磁通量的变化量为：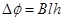
1分
回路中产生的感应电动势的平均值为：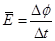
1分
回路中产生的感应电流的平均值为：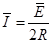
1分
通过导体棒横截面的电荷量为：
1分
系统产生的焦耳热为：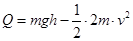
2分
联立以上各式解得：
1分
考点：法拉第电磁感应定律；能量守恒定律．
练习册系列答案
相关题目
（2008?福州模拟）如图所示，两根质量均为m=2kg的金属棒垂直地放在光滑的水平导轨上，左右两部分导轨间距之比为1：2，导轨间有大小相等但左右两部分方向相反的匀强磁场，CD棒电阻为AB棒电阻的两倍，不计导轨电阻，今用250N的水平力F向右拉CD棒，在CD棒运动0.5m的过程中，两棒上产生的焦耳热共为45J，此时CD棒速率为8m/s，立即撤去拉力F，设导轨足够长且两棒始终在不同磁场中运动，求：
（1）撤去外力时两棒的速度是多大？
