题目内容
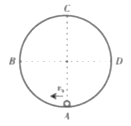
【题目】如图所示,半径为R的半圆形区域内,有垂直于坐标平面向里的匀强磁场,磁感应强度大小为B,半圆弧的圆心坐标为![]() ,圆弧与y轴相切于坐标原点。在坐标原点有一粒子源,可以向坐标平面内射出质量为m、电荷量大小为q的带负电的粒子,不计粒子重力。
,圆弧与y轴相切于坐标原点。在坐标原点有一粒子源,可以向坐标平面内射出质量为m、电荷量大小为q的带负电的粒子,不计粒子重力。
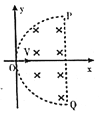
![]() 若粒子源沿x轴正方向射出不同速率的粒子,要使所有粒子不从直径PQ射出磁场,则粒子的速率最大是多少?
若粒子源沿x轴正方向射出不同速率的粒子,要使所有粒子不从直径PQ射出磁场,则粒子的速率最大是多少?
![]() 若粒子源向坐标平面内各个方向射出速率相同的粒子,要使所有粒子不从直径PQ射出磁场,则粒子的速率最大又是多少?
若粒子源向坐标平面内各个方向射出速率相同的粒子,要使所有粒子不从直径PQ射出磁场,则粒子的速率最大又是多少?
【答案】(1)![]() (2)
(2)![]()
【解析】
根据“不计重力的粒子飞出磁场”可知,本题考查带电粒子在磁场中运动的问题 ,根据匀速圆周运动规律,运用轨迹特点找到临界条件,列式分析推断.
(1)若粒子源沿x轴正方向射出不同速率的粒子,要使所有粒子不从直径PQ射出磁场,则速率最大的粒子运动轨迹如图所示:

由几何关系可知,粒子做圆周运动的半径为![]()
由牛顿第二定律,可知![]()
解得:![]()
(2)若粒子源向坐标平面内各个方向射出地率相同的粒子,粒子做圆动的半径相同,
则最容易从直径PQ射出的粒子源沿y轴正方向射出,该粒子刚好不从PQ射出的轨迹如图所示:
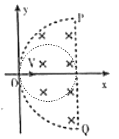
由几何关系可知,粒子做圆周运动的半径为![]()
由牛顿第二定律,可知![]()
解得:![]()

练习册系列答案
相关题目