��Ŀ����
13����ͼ��ʾ��S��һ��Դ����������г�����Ϊ5cm���γɵIJ������ʵ��������������ߴ�������֪��Դ��ʼ�������ģ��Ӵ�ʱ��ʼ��ʱ��t=0.4sʱ��һ���γɵIJ�����ͼ��ʾ��S��ನ��û������������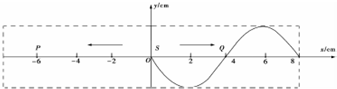
| A�� | ��ʱ�ʵ�Q����ƽ��λ�������� | |
| B�� | ��Դ��Ƶ��Ϊ$\frac{15}{4}$Hz | |
| C�� | �ò��IJ���Ϊ0.2m/s | |
| D�� | ͼ���ʵ�P��t=0.4sʱ���ڲ��� | |
| E�� | ��t=0��t=0.4s���ʵ�Q�˶���·��Ϊ20cm |
���� ����$f=\frac{1}{T}$���Ƶ�ʣ�����ͼ��ó�����������v=��f��Ⲩ�٣�������ͼ���ж��ʵ�P��t=0.4sʱ��λ�ã�һ����������·��Ϊ4A��
��� �⣺A�������Ҵ��������ݲ��Ĵ���ԭ�����ԣ���ʱQ������������A��ȷ��
B������ͼ���֪��0.4s�ڣ������ô�����һ������������T=0.4s��
��Դ��Ƶ��$f=\frac{1}{T}=\frac{1}{0.4}=2.5Hz$����B����
C������ͼ��ó�������=8cm=0.08m������v=��f=0.2m/s����C��ȷ��
D�����ݶԳ��Կ�֪���ʵ�C��t=0.4sʱ������λ����x=6cm������λ����ͬ�������ڲ��崦����D����
E����t=0��t=0.4s���ʵ�Q�˶��˰�����ڣ��˶���·��s=2A=2��5cm=10cm����E����
��ѡ��AC
���� ���⿼�鲨��ͼ��Ҫע����ȷӦ�ò���ͼ���ʵ����ͼ��ע�����ּ���ϵ���ܸ���ͼ��ó�������֪��һ����������·��Ϊ4A���Ѷ����У�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
4���ס������ʵ�������������СΪF������������������䣬��������������ӵ�ԭ����2����ͬʱ����֮��ľ����Ϊԭ����$\frac{1}{2}$����ס������������������С����Ϊ��������
| A�� | $\frac{F}{8}$ | B�� | 4F | C�� | 8F | D�� | 12F |
1�� a��b��������ͬһ�ص���ͬһ��ֱ���˶������ٶ�-ʱ��ͼ����ͼ��ʾ��ͼ��b��һ�������ߣ��������ж���ȷ���ǣ�������
a��b��������ͬһ�ص���ͬһ��ֱ���˶������ٶ�-ʱ��ͼ����ͼ��ʾ��ͼ��b��һ�������ߣ��������ж���ȷ���ǣ�������
 a��b��������ͬһ�ص���ͬһ��ֱ���˶������ٶ�-ʱ��ͼ����ͼ��ʾ��ͼ��b��һ�������ߣ��������ж���ȷ���ǣ�������
a��b��������ͬһ�ص���ͬһ��ֱ���˶������ٶ�-ʱ��ͼ����ͼ��ʾ��ͼ��b��һ�������ߣ��������ж���ȷ���ǣ�������| A�� | ����a��t1ʱ�̸ı��˶����� | |
| B�� | ��������t2ʱ������ | |
| C�� | ����b����������ļ���ֱ���˶� | |
| D�� | 0��t2�ڣ�����aһֱ������bǰ�棬t2ʱ�����������Զ |
8�� ��ͼ��ʾ����Դ�綯��ΪE���ڵ���Ϊr���������������Ļ�ƬPλ��a��ʱ���������еĴ���Һ��ǡ�ô��ھ�ֹ״̬���ڻ�Ƭ��a��b�ƶ��Ĺ��̣������ѹ��ʾ���仯���ľ���ֵΪ��U��������������仯���ľ���ֵΪ��I��������˵������ȷ���ǣ�������
��ͼ��ʾ����Դ�綯��ΪE���ڵ���Ϊr���������������Ļ�ƬPλ��a��ʱ���������еĴ���Һ��ǡ�ô��ھ�ֹ״̬���ڻ�Ƭ��a��b�ƶ��Ĺ��̣������ѹ��ʾ���仯���ľ���ֵΪ��U��������������仯���ľ���ֵΪ��I��������˵������ȷ���ǣ�������
 ��ͼ��ʾ����Դ�綯��ΪE���ڵ���Ϊr���������������Ļ�ƬPλ��a��ʱ���������еĴ���Һ��ǡ�ô��ھ�ֹ״̬���ڻ�Ƭ��a��b�ƶ��Ĺ��̣������ѹ��ʾ���仯���ľ���ֵΪ��U��������������仯���ľ���ֵΪ��I��������˵������ȷ���ǣ�������
��ͼ��ʾ����Դ�綯��ΪE���ڵ���Ϊr���������������Ļ�ƬPλ��a��ʱ���������еĴ���Һ��ǡ�ô��ھ�ֹ״̬���ڻ�Ƭ��a��b�ƶ��Ĺ��̣������ѹ��ʾ���仯���ľ���ֵΪ��U��������������仯���ľ���ֵΪ��I��������˵������ȷ���ǣ�������| A�� | ������ʾ���ȼ�С������$\frac{��U}{��I}$���� | |
| B�� | ����������ѹ��ʾ�����ȼ�С������ | |
| C�� | Һ�δ����磬�������������ٺ��������˶� | |
| D�� | Һ�δ����磬��һֱ�����������˶� |
18������������Ϊ�������ȷֲ������壻��֪��������������ٶ��������Ĵ�СΪg0���ڳ���Ĵ�СΪg��������ת������ΪT�����ڵ������Ͽ��Ƶ�����ط��е����ǵ����ٶ�Ϊ��������
| A�� | $\frac{T}{2��}$$\sqrt{g��{g}_{0}-g��}$ | B�� | $\frac{T}{2��}$$\sqrt{{g}_{0}��{g}_{0}-g��}$ | C�� | $\frac{T}{2��}$g | D�� | $\frac{T}{2��}$g0 |