题目内容
如图所示，水平面上质量均为4kg的两木块A、B用一轻弹簧相连接，整个系统处于平衡状态．现用一竖直向上的力F拉动木块A，使木块A向上做加速度为5m/s2的匀加速直线运动．选定A的起始位置为坐标原点，g=10m/s2，从力F刚作用在木块A的瞬间到B刚好离开地面的瞬间这个过程中，力F与木块A的位移x之间关系图象正确的是（ ）
A．
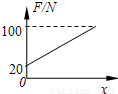
B．
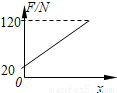
C．
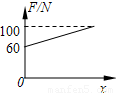
D．
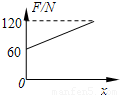
【答案】分析：最初弹簧被压缩，A物体受到竖直向上的弹力等于重力，由于A物体做匀加速直线运动，对A受力分析，列出牛顿第二定律解出对应的表达式；当B物体要离开地面时地面的支持力为零，弹簧对B物体向上的拉力等于B物体的重力，即弹簧对A物体向下的拉力等于B的重力，再列出牛顿第二定律解出此所需的拉力F大小即可．
解答：解：设初始状态时，弹簧的压缩量为x，弹簧劲度系数为k，物体的质量为m，则kx=mg；
力F作用在木块A上后，选取A为研究对象，其受到竖直向上的拉力F、竖直向下的重力mg和弹力k（x-x）三个力的作用，
根据牛顿第二定律，F+k（x-x）-mg=ma，即F=ma+kx=20+kx；
当弹簧对物体B竖直向上的弹力等于重力时B刚好离开地面，此时弹簧对物体A施加竖直向下的弹力F弹，大小为mg，
对物体A运用牛顿第二定律有F-mg-F弹=ma，
代入数据，可求得F=100N．
故选：A
点评：解决此类题时要注意胡克定律中弹簧的弹力与弹簧的形变量成正比，这里的形变量既可以是弹簧的伸长量，也可以是弹簧的压缩量．
解答：解：设初始状态时，弹簧的压缩量为x，弹簧劲度系数为k，物体的质量为m，则kx=mg；
力F作用在木块A上后，选取A为研究对象，其受到竖直向上的拉力F、竖直向下的重力mg和弹力k（x-x）三个力的作用，
根据牛顿第二定律，F+k（x-x）-mg=ma，即F=ma+kx=20+kx；
当弹簧对物体B竖直向上的弹力等于重力时B刚好离开地面，此时弹簧对物体A施加竖直向下的弹力F弹，大小为mg，
对物体A运用牛顿第二定律有F-mg-F弹=ma，
代入数据，可求得F=100N．
故选：A
点评：解决此类题时要注意胡克定律中弹簧的弹力与弹簧的形变量成正比，这里的形变量既可以是弹簧的伸长量，也可以是弹簧的压缩量．
练习册系列答案
阅读快车系列答案
相关题目
（2012?浠水县模拟）如图所示，水平面上有一固定着轻质定滑轮O的木块A，它的上表面与水平面平行，它的右侧是一个倾角θ=37°的斜面．放置在A上的物体B和物体C通过一轻质细绳相连，细绳的一部分与水平面平行，另一部分与斜面平行．现对A施加一水平向右的恒力F．使A、B、C恰好保持相对静止．已知A、B、C的质量均为m，重力加速度为g，不计一切摩擦，求恒力F的大小．（sin37°=0.6，cos37°=0.8）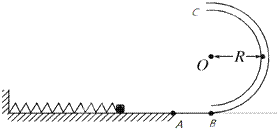
如图所示，水平面上某点固定一轻质弹簧，A点左侧的水平面光滑，右侧水平面粗糙，在A点右侧5m远处（B点）竖直放置一半圆形光滑轨道，轨道半径R=0.4m，连接处平滑．现将一质量m=0.1kg的小滑块放在弹簧的右端（不拴接），用力向左推滑块而压缩弹簧，使弹簧具有的弹性势能为2J，放手后，滑块被向右弹出，它与A点右侧水平面的动摩擦因数μ=0.2，取g=10m/s2，求：
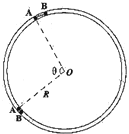如图所示，水平面上固定着一个半径R=0.4m的光滑圆环形轨道．在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和B（均可看作质点），两球间夹一轻质短弹簧（弹簧的长度相对环形轨道的半径和周长而言可忽略不计）．
的斜面。放置在A上的物体B和物体C通过一轻质细绳相连，细绳的一部分与水平面平行，另一部分与斜面平行。现对A施加一水平向右的恒力F，使A、B、C恰好保持相对静止。已知A、B、C的质量均为m，重力加速度为g，不计一切摩擦，求恒力F的大小。(
)