题目内容
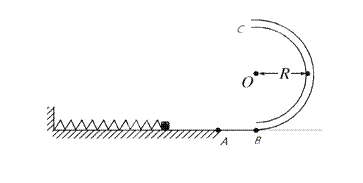
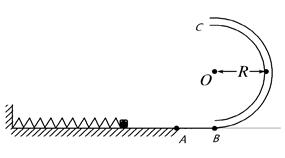
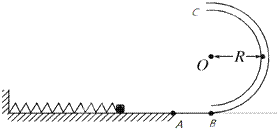 如图所示,水平面上某点固定一轻质弹簧,A点左侧的水平面光滑,右侧水平面粗糙,在A点右侧5m远处(B点)竖直放置一半圆形光滑轨道,轨道半径R=0.4m,连接处平滑.现将一质量m=0.1kg的小滑块放在弹簧的右端(不拴接),用力向左推滑块而压缩弹簧,使弹簧具有的弹性势能为2J,放手后,滑块被向右弹出,它与A点右侧水平面的动摩擦因数μ=0.2,取g=10m/s2,求:
如图所示,水平面上某点固定一轻质弹簧,A点左侧的水平面光滑,右侧水平面粗糙,在A点右侧5m远处(B点)竖直放置一半圆形光滑轨道,轨道半径R=0.4m,连接处平滑.现将一质量m=0.1kg的小滑块放在弹簧的右端(不拴接),用力向左推滑块而压缩弹簧,使弹簧具有的弹性势能为2J,放手后,滑块被向右弹出,它与A点右侧水平面的动摩擦因数μ=0.2,取g=10m/s2,求:(1)滑块运动到半圆形轨道最低点B处时对轨道的压力;
(2)改变半圆形轨道的位置(左右平移),使得被弹出的滑块到达半圆形轨道最高点C处时对轨道的压力大小等于滑块的重力,问AB之间的距离应调整为多少?
分析:(1)从小滑块被释放到达B点的过程中,据动能定理列式,在B点根据向心力公式列式,而弹力做的功等于弹簧具有的弹性势,联立方程即可求解;
(2)(2)在圆周最高点C处,滑块对轨道的压力等于其重力,包含两种情况:第一,当压力方向向上(滑块受到的支持力向下),第二,当压力方向向下(滑块受到的支持力向上),在C点根据向心力公式列式,整个过程中根据动能定理列式,联立方程即可求解.
(2)(2)在圆周最高点C处,滑块对轨道的压力等于其重力,包含两种情况:第一,当压力方向向上(滑块受到的支持力向下),第二,当压力方向向下(滑块受到的支持力向上),在C点根据向心力公式列式,整个过程中根据动能定理列式,联立方程即可求解.
解答:解:(1)从小滑块被释放到达B点的过程中,据动能定理有:W弹-μmgx=
mvB2
滑块在圆周轨道B点处,有:FN-mg=m
把W弹=△EP=2J数据代入,解得:FN=6N
由牛顿第三定律可知,滑块对轨道的压力大小为6N,方向竖直向下
(2)在圆周最高点C处,滑块对轨道的压力等于其重力,包含两种情况:
第一,当压力方向向上(滑块受到的支持力向下)时,
在C点处,有mg+N=m
整个过程有W-μmgx1-mg?2R=
mv02
把N=mg带入得:x1=4m
第二,当压力方向向下(滑块受到的支持力向上)时,
在C点处,有mg-N=m
整个过程有W-μmgx2-mg?2R=
mv02
把N=mg带入得:x2=6m
答:(1)滑块运动到半圆形轨道最低点B处时对轨道的压力为6N;
(2)改变半圆形轨道的位置(左右平移),使得被弹出的滑块到达半圆形轨道最高点C处时对轨道的压力大小等于滑块的重力,则AB之间的距离应调整为4m或6m.
| 1 |
| 2 |
滑块在圆周轨道B点处,有:FN-mg=m
| vB2 |
| R |
把W弹=△EP=2J数据代入,解得:FN=6N
由牛顿第三定律可知,滑块对轨道的压力大小为6N,方向竖直向下
(2)在圆周最高点C处,滑块对轨道的压力等于其重力,包含两种情况:
第一,当压力方向向上(滑块受到的支持力向下)时,
在C点处,有mg+N=m
| vC2 |
| R |
整个过程有W-μmgx1-mg?2R=
| 1 |
| 2 |
把N=mg带入得:x1=4m
第二,当压力方向向下(滑块受到的支持力向上)时,
在C点处,有mg-N=m
| vC2 |
| R |
整个过程有W-μmgx2-mg?2R=
| 1 |
| 2 |
把N=mg带入得:x2=6m
答:(1)滑块运动到半圆形轨道最低点B处时对轨道的压力为6N;
(2)改变半圆形轨道的位置(左右平移),使得被弹出的滑块到达半圆形轨道最高点C处时对轨道的压力大小等于滑块的重力,则AB之间的距离应调整为4m或6m.
点评:本题是动能定理与向心力公式的综合应用来处理圆周运动问题.利用功能关系解题的优点在于不用分析复杂的运动过程,只关心初末状态即可,平时要加强训练深刻体会这一点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目