题目内容
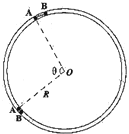 如图所示,水平面上固定着一个半径R=0.4m的光滑圆环形轨道.在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和B(均可看作质点),两球间夹一轻质短弹簧(弹簧的长度相对环形轨道的半径和周长而言可忽略不计).
如图所示,水平面上固定着一个半径R=0.4m的光滑圆环形轨道.在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和B(均可看作质点),两球间夹一轻质短弹簧(弹簧的长度相对环形轨道的半径和周长而言可忽略不计).(1)开始时,两球将轻质弹簧压缩,释放后,弹簧不动,两球沿轨道反方向运动一段时间后又第一次相遇.在此过程中,A球转过的角度θ是多少?
(2)如果压缩弹簧在弹开前储存的弹性势能E=1.2J,弹开后小球B在运动过程中受到的向心力是多大?
分析:(1)弹簧释放时,由系统动量守恒求得两球的速度关系,结合两球在同一个圆中运动,相遇时两球转过的角度正好是2π,可求解.
(2)对AB系统动量守恒可得到B的速度,从而可求向心力大小.
(2)对AB系统动量守恒可得到B的速度,从而可求向心力大小.
解答:解:(1)弹簧释放时,对AB两球,由动量守恒得:
MvA-mvB=0
得:vB=2vA
当两球第一次相遇时,满足ωAt+ωBt=2π
又:vA=ωAR vB=ωBR
所以:ωB=2ωA
代入上式得:3ωAt=2π
即:θ=
π
(2)弹簧释放时,由系统能量守恒得:
m
+
M
=E
vB=2vA
代入数据得vB=4m/s
对B:向心力F=
,
代入数据解得:F=4N.
答:(1)A球转过的角度
π;
(2)弹开后小球B在运动过程中受到的向心力是4N.
MvA-mvB=0
得:vB=2vA
当两球第一次相遇时,满足ωAt+ωBt=2π
又:vA=ωAR vB=ωBR
所以:ωB=2ωA
代入上式得:3ωAt=2π
即:θ=
| 2 |
| 3 |
(2)弹簧释放时,由系统能量守恒得:
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
vB=2vA
代入数据得vB=4m/s
对B:向心力F=
m
| ||
| R |
代入数据解得:F=4N.
答:(1)A球转过的角度
| 2 |
| 3 |
(2)弹开后小球B在运动过程中受到的向心力是4N.
点评:本题注意用整体法分析两球的运动,注意应用动量守恒和动能定理,可时解答简便.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图所示,两块固连在一起的物块a和b,质量分别是ma和mb.放在水平光滑桌面上,现同时施给他们方向如图所示的推力Fa和拉力Fb,已知Fa>Fb,则a对b的作用力( )
如图所示,两块固连在一起的物块a和b,质量分别是ma和mb.放在水平光滑桌面上,现同时施给他们方向如图所示的推力Fa和拉力Fb,已知Fa>Fb,则a对b的作用力( )



