题目内容
2. 如图所示:一质量为m、电荷量为-q的小球用轻质细线悬挂在O点,在匀强电场中处于静止状态,为使电场取得最小值,则电场强度的方向指向下方与竖直方向成$\frac{π}{2}-β$,大小为$\frac{mgsinβ}{q}$N/C.
如图所示:一质量为m、电荷量为-q的小球用轻质细线悬挂在O点,在匀强电场中处于静止状态,为使电场取得最小值,则电场强度的方向指向下方与竖直方向成$\frac{π}{2}-β$,大小为$\frac{mgsinβ}{q}$N/C.
分析 小球保持静止时受到重力、电场力和细线的拉力,运用作图法分析什么条件下电场力最小,再场强公式E=$\frac{F}{q}$得到场强的最小值.
解答 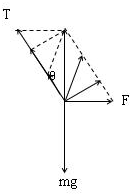 解:小球保持静止时受到重力mg、电场力F和细线的拉力T,作出受力图如图.根据作图法可知,当电场力F与细线垂直时,电场力最小,最小值为:F=mgsinβ
解:小球保持静止时受到重力mg、电场力F和细线的拉力T,作出受力图如图.根据作图法可知,当电场力F与细线垂直时,电场力最小,最小值为:F=mgsinβ
则场强的最小值为:E=$\frac{F}{q}$=$\frac{mgsinβ}{q}$ 因是负电荷则其方向与电场力的方向相反,与竖直向的夹角为($\frac{π}{2}-β$)
故答案为:下方 $\frac{π}{2}-β$ $\frac{mgsinβ}{q}$
点评 本题是物体平衡中极值问题,通过作图法得到极值的条件,也可以采用数学函数法求解极值.

练习册系列答案
相关题目
11.下列关于速度和加速度的说法中,正确的是( )
| A. | 加速度为负值,速度将减小 | |
| B. | 物体的速度为零,加速度也一定为零 | |
| C. | 运动物体的加速度越 来越小,物体运动的速度也越来越小 | |
| D. | 运动物体的加速度越来越小,表示速度变化越来越慢 |
10.下列关于弹力产生条件的说法中正确的是( )
| A. | 只要两个物体接触就一定有弹力产生 | |
| B. | 有摩檫力就一定有弹力产生 | |
| C. | 挂在电线下面的电灯受到向上的拉力,是因为电线发生微小的形变而产生的 | |
| D. | 形变大的物体产生的弹力一定比形变小的物体产生的弹力大 |
7. 一质量为0.1kg的小球自t=0时刻从水平地面上方某处自由下落,小球与地面碰后反向弹回,不计空气阻力,也不计小球与地面碰撞的时间,小球距地面的高度h与运动时间t关系如图所示,取g=10m/s2.则( )
一质量为0.1kg的小球自t=0时刻从水平地面上方某处自由下落,小球与地面碰后反向弹回,不计空气阻力,也不计小球与地面碰撞的时间,小球距地面的高度h与运动时间t关系如图所示,取g=10m/s2.则( )
 一质量为0.1kg的小球自t=0时刻从水平地面上方某处自由下落,小球与地面碰后反向弹回,不计空气阻力,也不计小球与地面碰撞的时间,小球距地面的高度h与运动时间t关系如图所示,取g=10m/s2.则( )
一质量为0.1kg的小球自t=0时刻从水平地面上方某处自由下落,小球与地面碰后反向弹回,不计空气阻力,也不计小球与地面碰撞的时间,小球距地面的高度h与运动时间t关系如图所示,取g=10m/s2.则( )| A. | 小球第一次与地面碰撞时机械能损失了5J | |
| B. | 小球第二次与地面碰撞前的最大速度为20m/s | |
| C. | 小球将在t=6s时与地面发生第四次碰撞 | |
| D. | 第二次碰撞后小球反弹过程中的最大势能(地面为零势能面)Ep=1.25J |
14. 如图所示,水平放置的两平行金属板长为L,间距为L,有一质量为m,电荷量为q的带电小球从原点沿x轴正方向进入两金属板.当小球运动点 ($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法正确的是 ( )
如图所示,水平放置的两平行金属板长为L,间距为L,有一质量为m,电荷量为q的带电小球从原点沿x轴正方向进入两金属板.当小球运动点 ($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法正确的是 ( )
 如图所示,水平放置的两平行金属板长为L,间距为L,有一质量为m,电荷量为q的带电小球从原点沿x轴正方向进入两金属板.当小球运动点 ($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法正确的是 ( )
如图所示,水平放置的两平行金属板长为L,间距为L,有一质量为m,电荷量为q的带电小球从原点沿x轴正方向进入两金属板.当小球运动点 ($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法正确的是 ( )| A. | 小球初速度大小为$\frac{2}{3}$$\sqrt{gL}$ | |
| B. | 两金属板间所加电压大小为$\frac{mgL}{2q}$ | |
| C. | 小球最终从点(L,L)处射出金属板 | |
| D. | 小球最终落在下金属板上的点(L,$\frac{5L}{6}$)位置处 |
11. 作用在同一物体上的三个力F1、F2、F3,现将三个共点力矢量首尾相连后,得到如图所示三角形,则这三个力的合力为( )
作用在同一物体上的三个力F1、F2、F3,现将三个共点力矢量首尾相连后,得到如图所示三角形,则这三个力的合力为( )
 作用在同一物体上的三个力F1、F2、F3,现将三个共点力矢量首尾相连后,得到如图所示三角形,则这三个力的合力为( )
作用在同一物体上的三个力F1、F2、F3,现将三个共点力矢量首尾相连后,得到如图所示三角形,则这三个力的合力为( )| A. | 0 | B. | 2F1 | C. | 2F2 | D. | 2F3 |
12. 如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前( )
如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前( )
 如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前( )
如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前( )| A. | 绳子拉力不变 | B. | 绳子拉力减小 | C. | AB杆受力增大 | D. | AB杆受力减小 |
 一定质量的理想气体按图示过程变化,其中bc与V轴平行,cd与T轴平行,则b→c过程中气体的内能不变(填“增加”“减小”或“不变”),气体的压强增加(填“增加”“减小”或“不变”),表示等压变化过程的是a→b(选填“a→b”、“b→c”或“c→d”).
一定质量的理想气体按图示过程变化,其中bc与V轴平行,cd与T轴平行,则b→c过程中气体的内能不变(填“增加”“减小”或“不变”),气体的压强增加(填“增加”“减小”或“不变”),表示等压变化过程的是a→b(选填“a→b”、“b→c”或“c→d”).