Question

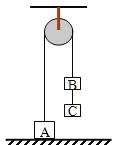
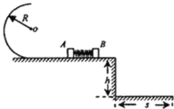
【题目】如图所示，光滑水平轨道距地面高h=0.8m，其左端固定有半径为R=0.6m的内壁光滑的半圆形轨道，轨道的最低点和水平轨道平滑连接．用质量分别为m1=1.0kg和m2=2.0kg的小物块A、B压缩一轻质弹簧（弹簧和和块不拴接）．同时放开小物块A、B，两物块和弹簧分离后，物块A进入圆形轨道，物块B从水平轨道右侧边缘飞出，其落地点到轨道边缘的水平距离s=1.2m．重力加速度g=10m/s2．

（1）物块B和弹簧分离的瞬间，物块B的速度大小；

（2）物块A运动到半圆形轨道最高点时，对轨道的压力．

（3）释放物块前弹簧具有的性势能．

Answer 1

【答案】（1）3m/s；（2）10N，方向竖直向上；（3）27J；

【解析】

（1）B离开水平轨道后做平抛运动，在竖直方向上：

水平方向：

联立并代入数据解得：

；

（2）A、B碰撞过程动量守恒，以A的初速度方向为正方向，由动量守恒定律得：

对A，由机械能守恒定律得：

在最高点，由牛顿第二定律得：

代入数据解得：

由牛顿第三定律可知，小物块对轨道的压力为10N，方向竖直向上；
（3）对系统，由能量守恒定律得：

代入数据解得：

。