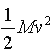题目内容
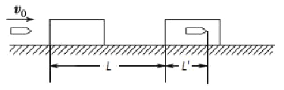
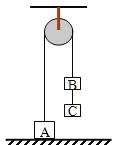
【题目】如图所示,物块A的质量为M,将A按住静止于地面,物块B、C的质量都是m,并都可看作质点,且m<M<2m。三物块用细线通过滑轮连接,物块B与物块C的距离和物块C到地面的距离都是L。现将物块A释放,若物块A距滑轮足够远且不计一切阻力。求:
(1)物块A上升过程中的最大速度;
(2)物块A上升的最大高度。
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)当物体C着地时,A具有最大速度,由机械能守恒得:
2mgL-MgL =![]() (2m+M)vm2
(2m+M)vm2
解得:![]()
(2)因为m<M,所以C着地后A、B做减速运动,设物体B刚着地时,A的速度为0,到达最高,根据机械能守恒定律有:![]() (M+m)vm2 = MgL-mgL
(M+m)vm2 = MgL-mgL
解得:![]() H1 = 2L
H1 = 2L
若![]() B末着地前速度已减速为零,设此时上升的高度为L1
B末着地前速度已减速为零,设此时上升的高度为L1
根据机械能守恒定律有:![]() (M+m)vm2 = MgL1-mgL1
(M+m)vm2 = MgL1-mgL1
H2 = L+L1
解得:![]()
若![]() 物体B着地时,M的速度不为0,仍在升高,设B着地时AB的速度为v2,B着地后A继续上升的高度为h,根据机械能守恒定律有:
物体B着地时,M的速度不为0,仍在升高,设B着地时AB的速度为v2,B着地后A继续上升的高度为h,根据机械能守恒定律有:
![]() (M+m)vm2-
(M+m)vm2-![]() (M+m)v22 = MgL-mgL
(M+m)v22 = MgL-mgL
![]() Mv22 =Mgh
Mv22 =Mgh
H3 = 2L+h
解得:![]()

练习册系列答案
相关题目