题目内容
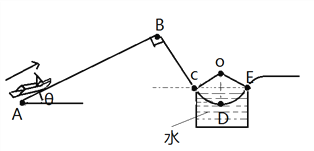
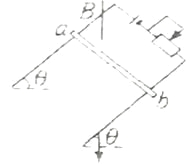
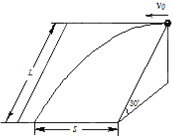
【题目】光滑曲面轨道置于高度为H=1.8 m的平台上,其末端切线水平;另有一长木板两端分别搁在轨道末端点和水平地面间,构成倾角为θ=37°的斜面,如图所示.一个可视作质点的质量为m=1 kg的小球,从光滑曲面上由静止开始下滑(不计空气阻力,g取10 m/s2,sin 37°≈0.6,cos 37°≈0.8)

(1)若小球从高h=0.2 m处下滑,则小球离开平台时速度v0的大小是多少?
(2)若小球下滑后正好落在木板的末端,则释放小球的高度h为多大?
(3)试推导小球下滑后第一次撞击木板时的动能与它下滑高度h的关系表达式。
【答案】(1)2 m/s (2)0.8 m (3)Ek=32.5h
【解析】
(1)小球从曲面上滑下,只有重力做功,由机械能守恒定律知:mgh=![]() m
m![]() ,得v0=
,得v0=![]() =
=![]() m/s=2 m/s.
m/s=2 m/s.
(2)小球离开平台后做平抛运动,小球正好落在木板的末端,则H=![]() gt2 ,
gt2 ,![]() =v1t联立两式得:v1=4 m/s,设释放小球的高度为h1,则由动能定理得:mgh1=
=v1t联立两式得:v1=4 m/s,设释放小球的高度为h1,则由动能定理得:mgh1=![]() m
m![]() ,解得h1=
,解得h1=![]() =0.8 m.
=0.8 m.
(3)由机械能守恒定律可得:mgh=![]() mv2,小球离开平台后做平抛运动,可看做水平方向的匀速直线运动和竖直方向的自由落体运动,则根据平抛运动规律:y=
mv2,小球离开平台后做平抛运动,可看做水平方向的匀速直线运动和竖直方向的自由落体运动,则根据平抛运动规律:y=![]() gt2,x=vt,几何关系:tan 37°=
gt2,x=vt,几何关系:tan 37°=![]() ,竖直速度:vy=gt,运动的合成:
,竖直速度:vy=gt,运动的合成:![]() =v2+
=v2+![]() ,动能:Ek=
,动能:Ek=![]() m
m![]() ,根据动能定理:mgh=
,根据动能定理:mgh=![]() mv2联立以上方程得:Ek=32.5h
mv2联立以上方程得:Ek=32.5h

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目