题目内容
【题目】某工厂用倾角为θ=37°的传送带把货物由低处运送到高处,已知传送带总长为L=50m,正常运转的速度为V=4m/s;某一次由于停电,工人把M=10kg的货物放在一块质量m=5kg带有挂钩的木板上,如图,通过定滑轮用平行传送带的绳子把木板拉上去。货物与木板及木板与传送带之间的动摩擦因数均为μ=0.8,(物块与木板均可视为质点,g=10m/s2,sin37°=0.6,cos37°=0.8)
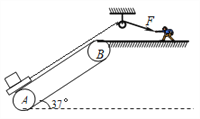
(1)为了把货物尽快拉上去又不使货物相对木板滑动,木板的最大加速度?
(2)若工人用F=189N的恒定的拉力把货物拉到L/5处来电了,工人随即撤去拉力,求此时货物与木板的速度?
(3)若来电瞬间传送带就达到了正常运转的速度为V=4m/s,求还需要多长时间货物到到达B处.
【答案】(1) ![]() (2)
(2)![]() (3)
(3) ![]()
【解析】(1)设最大拉力为Fm,货物与木板之间的静摩擦力达到最大值,设此时的加速度为a1,对货物分析根据牛顿第二定律得:
μMgcosθ-Mgsinθ=Ma1
代入数据得:a1=0.4m/s2
(2)设工人拉木板的加速度为a2,根据牛顿第二定律得:
F-μ(m+M)gcosθ-(m+M)gsinθ=(m+M)a2
代入数据解得:a2=0.2m/s2
设来电时木板的速度为v1,根据运动学公式得:v12=2a2![]()
代入数据得:v1=2m/s
(3)由于v1<4m/s,所以来电后木板继续加速,加速度为a3
μ(m+M)gcosθ-(m+M)gsinθ=(m+M)a3
代入数据得:a3=0.4m/s2
设经过t1木板速度与传送带速度相同,v=v1+a3t1
得:t1=5s
设t1内木板加速的位移为x1,v2v12=2a3x1
得:x1=15m
共速后,木板与传送带相对静止一起匀速运动,设匀速运动的时间为t2,匀速运动的位移为x2,x2=l![]() x1
x1
得:x2=25m
又:![]()
得:t2=6.25s
所以来电后木板再需要运动的时间为:t1+t2=11.25s.