题目内容
用轻弹簧连接在一起质量相等的两滑块A、B，静止在光滑的水平面上．现给滑块B一个向右的初速度，此后（ ）分析：对两物块进行受力分析，由牛顿第二定律可知两滑块的加速度大小关系；由运动过程分析可知两物体的速度大小关系．
解答：解：A、B有了速度之后，通过压缩弹簧而产生了弹力，则A向右加速，而B向右减速，当二者达到最大压缩量时，两物体的速度相等，故A错误；
B、达到最大压缩量后，A继续加速，而B继续减速；则AB间的距离变大，直到达到原长，此后A开始减速而B开始加速，但二者的距离仍在增大；当达到最大距离时二者速度应相同；故B正确；
C、由B的分析可知，当形变量消失时，AB的速度不相等，故C错误；
D、当形变消失时，B的速度最小；但是由于两物体的质量相同；故滑块A的速度一定与滑块B的初速度相等；
故选BD．
B、达到最大压缩量后，A继续加速，而B继续减速；则AB间的距离变大，直到达到原长，此后A开始减速而B开始加速，但二者的距离仍在增大；当达到最大距离时二者速度应相同；故B正确；
C、由B的分析可知，当形变量消失时，AB的速度不相等，故C错误；
D、当形变消失时，B的速度最小；但是由于两物体的质量相同；故滑块A的速度一定与滑块B的初速度相等；
故选BD．
点评：本题解题重点：一、应明确弹簧两端的弹簧大小相等；二、熟练掌握弹簧类问题变加速运动的过程．
练习册系列答案
发散思维新课堂系列答案
相关题目
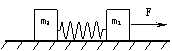
如图所示，质量为m1和m2的两物块放在光滑的水平地面上．用轻质弹簧将两物块连接在一起．当用水平力F作用在m1上时，两物块均以加速度a做匀加速运动，此时，弹簧伸长量为x，若用水平力F’作用在m1上时，两物块均以加速度a’=2a做匀加速运动．此时弹簧伸长量为x’．则下列关系正确的是（ ）
斜面上有m1和m2两个物体，与斜面间的动摩擦因数分别为μ1和μ2，两物体间用一根轻质弹簧连接，一起沿斜面减速上滑，如右图所示，在一起上滑的过程中，m1和m2之间的相对距离保持不变，弹簧的长度小于原长，则以下说法正确的是（ ）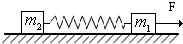
如图所示，质量分别为m1和m2的两物块放在水平地面上．与水平地面间的动摩擦因数都是μ（μ≠0），用轻质弹簧将两物块连接在一起．当用水平力F作用在m1上时，两物块均以加速度a做匀加速运动，此时，弹簧伸长量为x；若改用水平力F′=2F作用在m1上时．两物块均以加速度a′做匀加速运动，此时，弹簧伸长量为x′．则下列关系式中正确的是（ ）