��Ŀ����
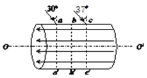
����Ŀ����ͼ��ʾ��ƽ��ֱ������ϵ![]() ���ڵ�I��������ƽ����
���ڵ�I��������ƽ����![]() �����ǿ�糡��������
�����ǿ�糡��������![]() ���������ڵ�IV������һ��
���������ڵ�IV������һ��![]() �����е�Բ����ǿ�ų�����ͼ��δ������������ֱ��
�����е�Բ����ǿ�ų�����ͼ��δ������������ֱ��![]() ƽ�������СΪ
ƽ�������СΪ![]() ��һ����Ϊ
��һ����Ϊ![]() �������Ϊ
�������Ϊ![]() �����ӣ���
�����ӣ���![]() ���ϵ�
���ϵ�![]() �㣬�Դ�СΪ
�㣬�Դ�СΪ![]() ���ٶ���
���ٶ���![]() ������������糡��ͨ���糡���
������������糡��ͨ���糡���![]() ���ϵ�
���ϵ�![]() ������IV����Բ����ǿ�ų��������ų����
������IV����Բ����ǿ�ų��������ų����![]() ���ϵ�ij������III���ޣ����ٶ���
���ϵ�ij������III���ޣ����ٶ���![]() �Ḻ�����45��ǣ������������ܵ���������
�Ḻ�����45��ǣ������������ܵ���������
��1���糡ǿ��![]() �Ĵ�С��
�Ĵ�С��
��2��Բ�δų�����С�����
��3�����Ӵ�![]() ���˶���ʼ�����ٴξ���
���˶���ʼ�����ٴξ���![]() ����������ʱ�䡣
����������ʱ�䡣
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
��������
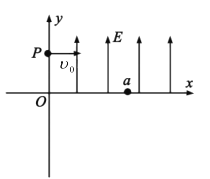
��1�������ڵ糡������ƽ���˶���
ˮƽ����
2h=v0t
��ֱ����
![]()
��ã�
![]()
��2�����ӵ���a��ʱ��y�᷽��ķ��ٶȣ�
![]()
���ӵ���a��ʱ���ٶȣ�
![]()
������x��������н�Ϊ45��.
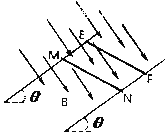
�����ڴų�����Բ���˶����˶��켣��ͼ��ʾ
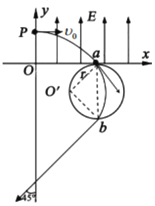
�����˶��켣Բ��Ӧ�����䷽����ٶȡ����䷽����ٶ����У�O�����������������Բ���˶���Բ�ġ������������еĹ켣����O��ΪԲ�ġ�rΪ�뾶��Բ�ϵ�Բ��ab��a���b��Ӧ������Բ�δų�����ı߽��ϡ�
��ͨ��a��b����IJ�ͬԲ���У���С��һ������ab����Ϊֱ����Բ�ܣ���Բ�δų��İ뾶ΪR�������ڴų�����Բ���˶������������ṩ����������ţ�ٵڶ����ɵã�
![]()
�ɼ��ι�ϵ��֪��Բ�δų��������С�뾶��
R=rsin45��
Բ�δų��������С�����S=��R2����ã�
![]() ��
��
��3�������ڵ糡�е��˶�ʱ�䣺
![]()
�����ڴų��е��˶�ʱ�䣺
![]()
�����뿪�ų���������ֱ���˶�������y����Ҫ��ʱ�䣺
![]()
�����ܵ��˶�ʱ�䣺
![]() ��
��