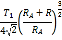Question

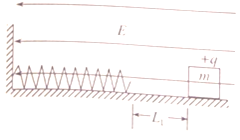
【题目】某控制带电粒子运动的仪器原理如图所示，区域PP′M′M内有竖直向下的匀强电

场，电场场强E＝1.0×103V/m，宽度d＝0.05m，长度L＝0.40m；区域MM′N′N内有垂直纸面向里的匀强磁场，磁感应强度B＝2.5×10－2T，宽度D＝0.05m，比荷＝1.0×108C/kg的带正电的粒子以水平初速度v0从P点射入电场．边界MM′不影响粒子的运动，不计粒子重力．

(1) 若v0＝8.0×105m/s，求粒子从区域PP′N′N射出的位置；

(2) 若粒子第一次进入磁场后就从M′N′间垂直边界射出，求v0的大小；

(3) 若粒子从M′点射出，求v0满足的条件．

Answer 1

【答案】(1)0.0125m (2) 3.6×105m/s. (3) 第一种情况：v0＝ (其中n＝0、1、2、3、4)第二种情况：v0＝ (其中n＝0、1、2、3)．

【解析】

(1) 粒子以水平初速度从P点射入电场后，在电场中做类平抛运动，假设粒子能够进入磁场，则

竖直方向

得

代入数据解得t＝1.0×10－6s

水平位移x＝v0t

代入数据解得x＝0.80m

因为x大于L，所以粒子不能进入磁场，而是从P′M′间射出，

则运动时间t0＝＝0.5×10－6s，

竖直位移＝0.0125m

所以粒子从P′点下方0.0125m处射出．

(2) 由第一问可以求得粒子在电场中做类平抛运动的水平位移x＝v0

粒子进入磁场时，垂直边界的速度

v1＝·t＝

设粒子与磁场边界之间的夹角为α，则粒子进入磁场时的速度为v＝

在磁场中由qvB＝m得R＝

粒子第一次进入磁场后，垂直边界M′N′射出磁场，必须满足x＋Rsinα＝L

把x＝v0、R＝、v＝、 代入解得

v0＝L·－

v0＝3.6×105m/s.

(3) 由第二问解答的图可知粒子离MM′的最远距离Δy＝R－Rcosα＝R(1－cosα)

把R＝、v＝、代入解得

可以看出当α＝90°时，Δy有最大值，(α＝90°即粒子从P点射入电场的速度为零，直接在电场中加速后以v1的速度垂直MM′进入磁场运动半个圆周回到电场)

Δymax＝0.04m，Δymax小于磁场宽度D，所以不管粒子的水平射入速度是多少，粒子都不会从边界NN′射出磁场．

若粒子速度较小，周期性运动的轨迹如下图所示：

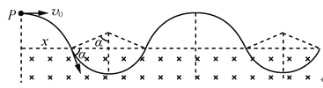
粒子要从M′点射出边界有两种情况，

第一种情况：

L＝n(2v0t＋2Rsinα)＋v0t

把、R＝ 、v1＝vsinα、 代入解得

v0＝×105m/s(其中n＝0、1、2、3、4)

第二种情况：

L＝n(2v0t＋2Rsinα)＋v0t＋2Rsinα

把 、R＝、v1＝vsinα、代入解得

v0＝×105m/s(其中n＝0、1、2、3)．