题目内容
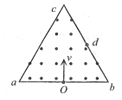
【题目】如图所示，正三角形abc区域内存在着方向垂直于纸面向外的匀强磁场，三角形的边长为4L．一个带电粒子（重力不计）从ab边的中点O以垂直于ab边的速度v进入磁场，粒子恰好从bc边的中点d飞出磁场，若将该粒子进入磁场的速度方向从图示位置逆时针旋转60°，同时改变速度的大小，发现粒子仍可以从d点飞出磁场。下列说法不正确的是（ ）
A. 第二次粒子的速度大小应为
B. 第二次粒子在磁场中运动时间是第一次的2倍
C. 两次粒子从d点飞出磁场时速度方向夹角为
D. 粒子两次做圆周运动的圆心间距为
【答案】B
【解析】
粒子在磁场中只受洛伦兹力作用，故粒子做匀速圆周运动，洛伦兹力做向心力，故有：qvB=m
；粒子垂直ab边从O点发射，从d点离开磁场，根据几何关系可得：轨道圆心为b点，粒子垂直bc边离开磁场，轨道半径r1=2L，转过的圆心角为60°；改变粒子发射方向后，根据几何关系可得：轨道圆心为Od中点，粒子刚好转过180°，轨道半径r2=L，粒子从d点离开磁场时的速度方向刚好和发射方向相反，与db边成30°，斜向右下；根据洛伦兹力做向心力可得：轨道半径
，所以，v2：v=r2：r1=1：2，所以，第二次粒子的速度大小
，故A正确；根据洛伦兹力做向心力可得：圆周运动周期
，故两次运动周期相等，那么，由转过的圆心角可得：第二次粒子在磁场中运动时间是第一次的3倍，故B错误；根据第一次粒子垂直bc边离开磁场，第二次粒子从d点离开磁场时的速度方向刚好和发射方向相反，与db边成30°，斜向右下；所以，两次粒子从d点飞出磁场时速度方向夹角为60°，故C正确；根据第一次的轨道圆心为b点，第二次的轨道圆心为Od中点，由几何关系可得：粒子两次做圆周运动的圆心间距为
L，故D正确；本题选不正确的，故选B.
