Question

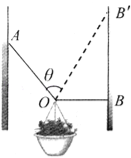
【题目】两束平行的、同频率的红色细激光束，垂直于半圆柱玻璃的平面射到半圆柱玻璃上，如图所示．已知其中一条光线始终不改变传播方向穿过玻璃，它的入射点是O；另一条光线的入射点为A，穿过玻璃后两条光线交于P点．已知玻璃截面的圆半径为R，OA= ，OP= R．求：

①玻璃材料对该红光的折射率；
②光从A点到达P点的时间．

Answer 1

【答案】解：①作出光路如图所示，其中一条光线沿直线穿过玻璃，可知O点为圆心；另一条光线沿直线进入玻璃，在半圆面上的入射点为B，入射角设为θ1，折射角设为θ2．

则sinθ1= =

得：θ1=30°

因OP= R，由几何关系知 BP=R，则折射角为：θ2=60°

由折射定律得玻璃的折射率为：n= = = =1.73

②光在玻璃内传播的速度为：v= = c

光在玻璃内从A到B间的距离为：L1=Rcos30°= R

光在玻璃内传播的时间为：t1= = =

BP间的距离为：L2=R，

光从B点传播到P点的时间为：t2= =

光从A点到达P点的时间为：t=t1+t2=

答：①玻璃材料对该红光的折射率为1.73；

②光从A点到达P点的时间是 ．

【解析】（1）光线沿直线穿过玻璃，可知O点为圆心，另一条光线沿直线进入玻璃，只发生一次折射，根据几何关系求出折射角，再根据折射定律求出玻璃的折射率；
（2）先求光在玻璃内传播的速度，再求光在玻璃内传播的时间，最后根据BP间的距离求光从B点传播到P点的时间，两个时间相加即为光从A点到达P点的时间。