题目内容
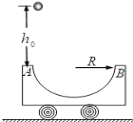
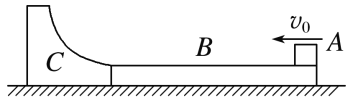
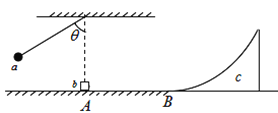
【题目】如图所示，小球（可视为质点）用非弹性悬线吊在天花板上，在悬点正下方A点处有一物块b（可视为质点）放在水平地面上，一质量为2m光滑曲面滑块c与地面在B点平滑连接，小球a的质量为m，物块b的质量为2m，物块b与B点左侧的水平地面的动摩擦因数为
，B点右侧的水平地面光滑。将小球拉到悬线与竖直方向的夹角为
的位置由静止时放，小球运动到最低点时刚好与物块发生弹性碰撞，碰后物块能滑到曲面上某一最大高度处。悬线长为L，A、B两点的距离也为L，重力加速度为g，求：
（1）碰后小球a再次摆动的最大高度；
（2）碰后物块b滑上曲面c的最大高度。
【答案】（1）
（2）
【解析】
(1)设小球与物块碰撞前速度为v1，根据机械能守恒有
解得：
小球与物块碰撞过程动量守恒、能量守恒，有
解得
设碰后小球摆动的最大高度为h1
解得
(2)物块在地面上运动时的加速度大小a=μg
设物块运动到B点的速度为：
设物块能滑上曲面的最大高度为h2，此时b与c共速，根据水平方向上动量守恒可知：
根据能量守恒可知
解得：
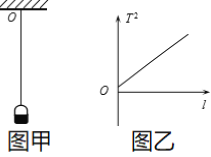
阅读快车系列答案
【题目】用单摆测定重力加速度的实验装置如图所示。
（1）组装单摆时，应在下列器材中选用_______（选填选项前的字母）。
A．长度为1m左右的细线
B．长度为30cm左右的细线
C．直径为1.5cm左右的塑料球
D．直径为1.5cm左右的小钢球
（2）在实验中，有人提出以下几点建议，其中合理的是________（选填选项前的字母）。
A．测摆线长时，应让小球静止在平衡位置，测量悬点到小球顶点的距离
B．单摆偏离平衡位置的角度不能太大，摆角θ＜5°
C．在摆球经过最低点时启动秒表计时
D．用秒表记录摆球一次全振动的时间作为周期
（3）某次实验时，测得摆线长为l，小球的直径为d，单摆完成n次全振动所用的时间为t，则重力加速度g =________（用已知物理量表示表示）。
（4）下表是甲同学记录的3组实验数据，并做了部分计算处理。
组次 | 1 | 2 | 3 |
摆线长l/mm | 793.0 | 893.0 | 993.0 |
小球直径d/mm | 14.0 | 14.0 | 14.0 |
50次全振动时间t/s | 90.0 | 95.5 | 100.5 |
振动周期T/s | 1.80 | 1.91 | |
重力加速度g/( | 9.74 | 9.73 |
请计算出第3组实验中的T =________s，g =/span>________m/s2。
（5）乙同学用多组实验数据做出周期的平方（T2）与摆长（L）关系的图像，如图所示，图像是一条过原点的直线，斜率为k。由此可知重力加速度g=________。
（6）丙同学在家里测重力加速度。他用细线和小铁锁制成一个单摆，如图甲所示。由于他无法确定铁锁的重心位置，所以他只测得摆线的长度l。然后将铁锁拉离平衡位置一个小角度由静止释放，测出振动周期T。多次改变摆线的长度，重复上面操作，得到多组l、T的数据，作出T2－l图像如图乙所示，图像是一条不过原点的直线。他借鉴乙同学的思路，结合直线的斜率求得重力加速度。丙同学得到的重力加速度是否正确？并说明理由________.（可忽略空气阻力对该实验的影响）
