题目内容
如图1所示,一长为l且不可伸长的绝缘细线,一端固定于O点,另一端拴一质量为m的带电小球。空间存在一场强为E、方向水平向右的匀强电场。当小球静止时,细线与竖直方向的夹角为θ=37°。已知重力加速度为g,sin37°=0.6,cos37°=0.8。


(1)判断小球所带电荷的性质,并求出小球所带的电荷量q;
(2)如图2所示,将小球拉至A点,使细线处于水平拉直状态。释放小球,小球由静止开始向下摆动,当小球摆到B点时速度恰好为零。
a.求小球摆动过程中最大速度vm的大小;
b.三位同学对小球摆动到B点时所受合力的大小F合进行了讨论:第一位同学认为 ;第二位同学认为F合<mg;第三位同学认为F合=mg。你认为谁的观点正确?请给出证明。
;第二位同学认为F合<mg;第三位同学认为F合=mg。你认为谁的观点正确?请给出证明。
(1)正电荷  (2)a.
(2)a.  b. 第三位同学的观点正确
b. 第三位同学的观点正确
【解析】
试题分析:(1)小球静止时的位置受力平衡可判断电场力水平向右与电场同向,所以小球带正电。
因为 
所以  (6分)
(6分)
(2)a.小球在场中静止时的位置是小球摆动过程中的平衡位置,故小球到达此位置时速度最大。根据动能定理有
所以  (6分)
(6分)
b.第三位同学的观点正确。 (2分)

【方法一】根据对称性,小球摆到B点时所受的合力与小球在A点时所受合力的大小相等。小球到达A点时的受力如图所示,因为TA=qE,所以小球所受合力的大小F合=mg。
【方法二】设小球摆到B点时,细线与竖直方向的夹角为α,根据动能定理有

又因为  ,所以
,所以 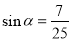 ,
,
则  (6分)
(6分)
考点:电场 共点力的平衡 功能关系

练习册系列答案
相关题目


















