题目内容
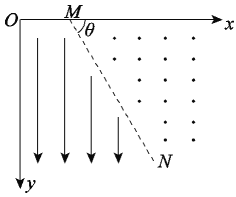
【题目】在如图所示的平面直角坐标系xOy中,x轴上有一点M(x0,0),过M点的直线MN与x轴的夹角θ=60°,在MN的左侧区域有竖直向下的匀强电场,MN的右侧区域有垂直纸面向外的匀强磁场。从O点以速度v0沿x轴正方向水平射出一带电粒子P,同时从M点以另一速度沿x轴正方向水平射出另一带电粒子Q,经过一段时间两粒子在直线MN上的D点(未画出)相遇(不相撞)。已知粒子P恰不能越过直线MN,两粒子质量、电量完全相同,均带正电,不计粒子重力。求:
(1)粒子P、Q射出后多长时间相遇?
(2)带电粒子Q射出时速度的大小。
【答案】(1) t=![]() (2) v=
(2) v=![]() v0
v0
【解析】
(1)两粒子射出后,运动的轨迹如图所示:
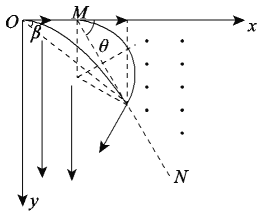
粒子P恰不能越过直线,粒子运动到直线上时速度方向沿MN方向,速度的反向延长线交x轴于M点,粒子P在电场中做类平抛运动,设位移偏转角为β,由
y=![]() at2 ①
at2 ①
x=v0t ②
vy=at ③
tan β=![]() ④
④
tan θ=![]() ⑤
⑤
联立可得,粒子P的水平位移
x=2x0
粒子P、Q相遇的时间
t=![]()
(2)粒子Q在右侧磁场区域做匀速圆周运动,粒子的轨迹半径
r=![]()
粒子Q运动路程
s=![]()
粒子Q运动时间
t=![]()
根据题意,粒子P、Q运动时间相同,联立可得粒子Q抛出时的速度
v=![]() v0
v0

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目