题目内容
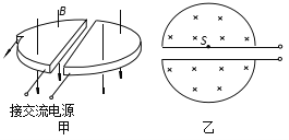
【题目】在高能物理研究中,粒子加速器起着重要作用,而早期的加速器只能使带电粒子在高压电场中加速一次,因而粒子所能达到的能量受到高压技术的限制。1930年,Earnest O. Lawrence提出了回旋加速器的理论,他设想用磁场使带电粒子沿圆弧形轨道旋转,多次反复地通过高频加速电场,直至达到高能量。图12甲为Earnest O. Lawrence设计的回旋加速器的示意图。它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条狭缝;两个D型盒处在匀强磁场中并接有高频交变电压。图乙为俯视图,在D型盒上半面中心S处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D型盒中。在磁场力的作用下运动半周,再经狭缝电压加速;为保证粒子每次经过狭缝都被加速,应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致。如此周而复始,最后到达D型盒的边缘,获得最大速度后被束流提取装置提取出。已知正离子的电荷量为q,质量为m,加速时电极间电压大小恒为U,磁场的磁感应强度为B,D型盒的半径为R,狭缝之间的距离为d。设正离子从离子源出发时的初速度为零。
(1)试计算上述正离子从离子源出发被第一次加速后进入下半盒中运动的轨道半径;
(2)尽管粒子在狭缝中每次加速的时间很短但也不可忽略。试计算上述正离子在某次加速过程当中从离开离子源到被第n次加速结束时所经历的时间;
【答案】(1) ![]() (2)
(2) ![]()
【解析】(1)设正离子经过窄缝被第一次加速加速后的速度为v1,
由动能定理得: ![]()
正离子在磁场中做匀速圆周运动,半径为r1,由牛顿第二定律得: ![]()
由以上两式解得: ![]()
故正离子从离子源出发被第一次加速后进入下半盒中运动的轨道半径为: ![]()
(2)设正离子经过窄缝被第n次加速加速后的速度为vn,
由动能定理得: ![]()
粒子在狭缝中经n次加速的总时间为: ![]()
由牛顿第二定律有: ![]()
由以上三式解得电场对粒子加速的时间为: ![]()
正离子在磁场中做匀速圆周运动,由牛顿第二定律有: ![]()
又因有: ![]()
粒子在磁场中做圆周运动的时间为: ![]()
由以上三式解得: ![]()
所以,粒子从离开离子源到被第n次加速结束时所经历的时间为: ![]()
故正离子在某次加速过程当中从离开离子源到被第n次加速结束时所经历的时间为![]()