题目内容
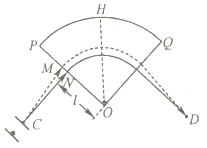
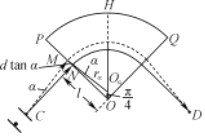
【题目】如图所示为一种质谱仪的工作原理图,圆心角为![]() 弧度的扇形OPQ区域内存在磁感应强度大小为B、方向垂直纸面向外的匀强磁场(图中未画出)。某种带电粒子由静止开始经电压为U的加速电场加速后从小孔C射出,从N点沿既垂直于OP又垂直于磁场方向进入磁场,然后从边界OQ射出,射出时速度方向与OQ垂直,其轨迹如图中实线所示,已知ON=l.
弧度的扇形OPQ区域内存在磁感应强度大小为B、方向垂直纸面向外的匀强磁场(图中未画出)。某种带电粒子由静止开始经电压为U的加速电场加速后从小孔C射出,从N点沿既垂直于OP又垂直于磁场方向进入磁场,然后从边界OQ射出,射出时速度方向与OQ垂直,其轨迹如图中实线所示,已知ON=l.
(1)求该粒子在磁场区域中运动的时间t。
(2)若被加速的粒子从小孔C射出瞬时又获得一个沿OP方向很小的速度,为使该粒子能沿图中的虚线运动,并在磁场区域右侧的D点被收集(D点与C点关于∠POQ的角平分线OH对称),则CN的长度d应调节为多长?
【答案】(1)![]() (2)d=l
(2)d=l
【解析】
(1)在电场中,由动能定理得:qU=![]() mv02
mv02
在磁场中,由洛伦兹力提供向心力得:qv0B=m![]() ,又由题意得:r=l
,又由题意得:r=l
粒子在磁场区域中运动的时间: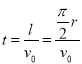 ,解得:
,解得:![]()
(2)由图可得vαcosα=v0
在磁场中,由洛伦兹力提供向心力得:qvαB=m![]() ,可得rαcosα=r=l
,可得rαcosα=r=l
由正弦定理得: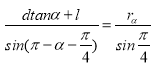
解得d=l

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目