题目内容
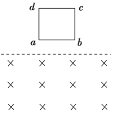
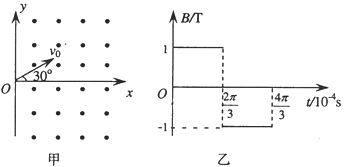
【题目】如图甲所示，在y轴右侧加有垂直纸面向外的匀强磁场，磁感应强度B=1T。从原点O处向第I象限发射一比荷
=1×104C/kg的带正电的粒子（重力不计）），速度大小v0=103m/s，方向垂直于磁场且与x轴正方向成30°角．
（1）求粒子在该匀强磁场中做匀速圆周运动的半径R和在该磁场中运动的时间t1．
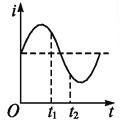
（2）若磁场随时间变化的规律如图乙所示（垂直于纸面向外为正方向），
后空间不存在磁场．在t=0时刻，粒子仍从O点以与原来相同的速度v0射入，求粒子从O点射出后第2次经过x轴时的坐标．
【答案】
【解析】
试题（1）粒子在磁场中运动，洛伦兹力提供向心力，由牛顿第二定律可求出粒子运动轨迹的半径．由带电粒子在匀强磁场中的周期公式
，可求出粒子的运动周期，通过题意找出磁场的变化周期和粒子的运动周期的关系，结合几何图形，可求出粒子运动的时间．
（2）结合前面的分析，考虑到带电粒子从运动中可完成的周期的重复性，列式求解即可．
（1）轨迹如图甲所示．由
得
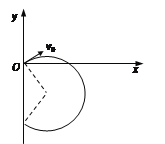
图甲
轨迹半径
（2分）
粒子运动周期
（2分）
粒子在磁场中轨迹所对的圆心角为240° ，
所以粒子在磁场中运动的时间为t1=
=
（2分）
（2）磁场变化的半周期为
（2分）
在图乙中，∠OO1C＝∠CO2D＝120°，且O1O2平行于x轴
OE＝2（R＋Rsin30°）＝3R＝0.3ｍ （2分）
RtΔEDP中，∠EDP＝60°，DE＝2Rsin60° （2分）
EP＝DEtan60°＝3R＝0.3ｍ （2分）
则粒子从O点射出后第2次经过x轴时的坐标xp＝OE＋EP＝0.6m （2分）
练习册系列答案
全能测控一本好卷系列答案
相关题目
