Question

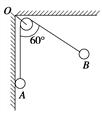
【题目】如图所示，A、B是系在绝缘细线两端、带有等量同种电荷的小球，其中mA＝0.1kg，细线总长为20cm，现将绝缘细线绕过固定于O点的光滑定滑轮，将两球悬挂起来，两球平衡时，OA的线长等于OB的线长，A球依在光滑绝缘竖直墙上，B球所在悬线OB偏离竖直方向60°，求B球的质量和墙所受A球的压力．(g取10m/s2)

Answer 1

【答案】B球的质量为0.2kg，墙所受A球的压力大小为1.732N，方向水平向左

【解析】试题分析：考查受力平衡，分别对A球和B球受力分析，运用力的合成或分解结合共点力平衡条件解决问题．

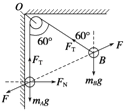
解：令两球之间的库仑斥力为F，绳中的张力为FT，画出两球的受力分析如图所示，由平衡条件对A球有：

FT﹣mAg﹣Fsin 30°=0，①

Fcos 30°﹣FN=0，②

对B由平衡条件得：

FT=F，③

F=mBg，④

由①②③④式得mB="0.2" kg，

FN="1.732" N，

由牛顿第三定律，墙所受A球压力大小

FN′=FN="1.732" N，方向水平向左．

答：B球的质量为0.2kg，墙所受A球的压力大小为1.732N，方向水平向左．