Question

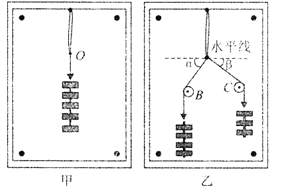
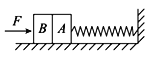
【题目】如图所示，劲度系数为k的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为m的物体A连接（另有一个完全相同的物体B紧贴着A，不粘连），弹簧水平且无形变。用水平力F缓慢推动物体B，在弹性限度内弹簧长度被压缩了x0，此时物体A、B静止。撤去F后，物体A、B开始向左运动，已知重力加速度为g，物体A、B与水平面间的动摩擦因数为μ。则

A. 撤去F瞬间，物体A、B的加速度大小为

B. 撤去F后，物体A和B先做匀加速运动，再做匀减速运动

C. 物体A、B一起向左运动距离时获得最大速度

D. 若物体A、B向左运动要分离，则分离时向左运动距离为

Answer 1

【答案】AC

【解析】A项：设撤去F后，物体刚运动时加速度为a，根据牛顿第二定律： ，解得，故A正确；

B项：撤去F后的一段时间内，由于运动过程中弹力不断变化，物体先做变加速运动，后做变减速运动，再做匀减速运动，故B错误；

C项：弹力与摩擦力大小相等时，速度最大，此时kx1＝2μmg，该过程物体向左运动的位移为，故C正确；

D项：物体A、B分离时，A、B间的弹力为零且加速度相等，由B受力分析可知，此时B的加速度，对A分析有： ，解得，所以A、B向左运动的位移为，故D错误。

点晴：解决本题关键找出弹力与摩擦力大小相等时，速度最大，根据合力为零求解，物体A、B分离时，A、B间的弹力为零且加速度相等。