题目内容
13. 如图所示,质量M=3.5kg的小车静止于光滑水平面上靠近桌子处,其上表面与水平桌面相平,小车长L=1.2m,其左端放有一质量为0.5kg的滑块Q.水平放置的轻弹簧左端固定,质量为1kg的小物块P置于桌面上的A点并与弹簧的右端接触.此时弹簧处于原长,现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=6J,撤去推力后,P沿桌面滑到小车上并与Q相碰,最后Q停在小车的右端,P停在距小车左端0.5m处.已知AB间距L1=5cm,A点离桌子边沿C点距离L2=90cm,P与桌面间动摩擦因数μ1=0.4,P、Q与小车表面间动摩擦因数μ2=0.1.(g=10m/s2)求:
如图所示,质量M=3.5kg的小车静止于光滑水平面上靠近桌子处,其上表面与水平桌面相平,小车长L=1.2m,其左端放有一质量为0.5kg的滑块Q.水平放置的轻弹簧左端固定,质量为1kg的小物块P置于桌面上的A点并与弹簧的右端接触.此时弹簧处于原长,现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=6J,撤去推力后,P沿桌面滑到小车上并与Q相碰,最后Q停在小车的右端,P停在距小车左端0.5m处.已知AB间距L1=5cm,A点离桌子边沿C点距离L2=90cm,P与桌面间动摩擦因数μ1=0.4,P、Q与小车表面间动摩擦因数μ2=0.1.(g=10m/s2)求:(1)P到达C点时的速度 vC.
(2)P与Q碰撞后瞬间Q的速度大小.
分析 (1)对ABC过程由动能定理可求得P到达C点时的速度;
(2)分别对PQ碰撞过程和整体由动量守恒定律列式,并对全过程由能量守恒列式,联立可求得PQ碰后瞬间Q的速度;注意计论各解是否符合实际.
解答 解:(1)对P由A→B→C应用动能定理,
得${W_F}-{μ_1}{m_1}g(2{L_1}+{L_2})=\frac{1}{2}{m_1}{v_C}^2$
解得:VC=2m/s
(2)设P、Q碰后速度分别为v1、v2,小车最后速度为v,向右为正方向,
由动量守恒定律得,m1vC=m1v1+m2v2
m1vC=(m1+m2+M)v
由能量守恒得,${μ_2}{m_1}gS+{μ_2}{m_2}gL=\frac{1}{2}{m_1}{v_1}^2+\frac{1}{2}{m_2}{v_2}^2-\frac{1}{2}({M+{m_1}+{m_2}}){v^2}$
解得,v2=2m/s
${v_2}^′=\frac{2}{3}m/s$
当${v_2}^′=\frac{2}{3}m/s$时,${v_1}=\frac{5}{3}m/s>{v_2}^′$不合题意,舍去.
即P与Q碰撞后瞬间Q的速度大小为v2=2m/s
答:(1)P到达C点时的速度 vC为2m/s.
(2)P与Q碰撞后瞬间Q的速度大小为2m/s.
点评 本题考查动量守恒定律及功能关系的综合应用,解题时要注意正确分析物理过程,明确各过程的受力及运动情况,优先应用动量守恒和动能定理进行分析求解.

练习册系列答案
相关题目
3. 如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为n1:n2=10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为μ1=220$\sqrt{2}$sin100πt(V),开始时,单刀双掷开关与a连接,下列说法中正确的是( )| A. | t=$\frac{1}{200}$时,cd间电压的瞬时值为220V | |
| B. | t=$\frac{1}{200}$ 时,电压表的示数为22V | |
| C. | 若将滑动变阻器的滑片向上移,电流变和电压表的示数都变小 | |
| D. | 当单刀双掷开关由a拨向b时,电压表和电流表的示数均变小 |
4. 如图所示,长为L的轻杆上端连着一质量为m的小球,杆的下端用铰链固接于水平面上的O点,轻杆处于竖直方向时置于同一水平面上质量为M的立方体恰与小球接触.对小球施加微小的扰动,使杆向右倾倒,当立方体和小球刚脱离接触的瞬间,杆与水平面的夹角恰好为$\frac{π}{6}$,忽略一切摩擦,( )
如图所示,长为L的轻杆上端连着一质量为m的小球,杆的下端用铰链固接于水平面上的O点,轻杆处于竖直方向时置于同一水平面上质量为M的立方体恰与小球接触.对小球施加微小的扰动,使杆向右倾倒,当立方体和小球刚脱离接触的瞬间,杆与水平面的夹角恰好为$\frac{π}{6}$,忽略一切摩擦,( )
 如图所示,长为L的轻杆上端连着一质量为m的小球,杆的下端用铰链固接于水平面上的O点,轻杆处于竖直方向时置于同一水平面上质量为M的立方体恰与小球接触.对小球施加微小的扰动,使杆向右倾倒,当立方体和小球刚脱离接触的瞬间,杆与水平面的夹角恰好为$\frac{π}{6}$,忽略一切摩擦,( )
如图所示,长为L的轻杆上端连着一质量为m的小球,杆的下端用铰链固接于水平面上的O点,轻杆处于竖直方向时置于同一水平面上质量为M的立方体恰与小球接触.对小球施加微小的扰动,使杆向右倾倒,当立方体和小球刚脱离接触的瞬间,杆与水平面的夹角恰好为$\frac{π}{6}$,忽略一切摩擦,( )| A. | 此时立方体M的速度达到最大 | B. | 此时小球m的加速度为零 | ||
| C. | 此时杆对小球m的拉力为零 | D. | M和m的质量之比为4:1 |
18.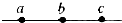 如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )
如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )
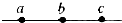 如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )
如图所示,沿波的传播方向上有间距均为1m的质点a、b、c,静止在各自的平衡位置,一列横波以1m/s的速度水平向右传播,t=0时质点a开始由平衡位置向上运动,t=1s时质点a第一次到达最高点.在8s<t<9s这段时间内质点c的状态是( )| A. | 速度逐渐增大 | B. | 加速度逐渐增大 | ||
| C. | 一直在向上运动 | D. | 先向下后向上运动 |
5. 如图所示,在绝缘水平面上固定两个等量同种电荷P、Q,在P、Q连线上的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N(未画出)而停下,则以下说法正确的是( )
如图所示,在绝缘水平面上固定两个等量同种电荷P、Q,在P、Q连线上的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N(未画出)而停下,则以下说法正确的是( )
 如图所示,在绝缘水平面上固定两个等量同种电荷P、Q,在P、Q连线上的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N(未画出)而停下,则以下说法正确的是( )
如图所示,在绝缘水平面上固定两个等量同种电荷P、Q,在P、Q连线上的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N(未画出)而停下,则以下说法正确的是( )| A. | 滑块受到的电场力一定是先减小后增大 | |
| B. | 滑块的电势能可能一直减小 | |
| C. | PM间距一定小于QN间距 | |
| D. | 滑块的动能与电势能之和可能保持不变 |
3.频率为50Hz的交变电流,其电压u=120$\sqrt{2}$sinωtV,把它加在激发电压、熄灭电压均为85V的霓虹灯的两段,则在半个周期内霓虹灯点亮的时间是( )
| A. | $\frac{1}{50}$s | B. | $\frac{1}{100}$s | C. | $\frac{1}{150}$s | D. | $\frac{1}{200}$s |

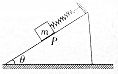 如图所示,倾角为θ的直角斜面体固定在水平地面上,一根轻质弹簧上端固定在斜面上,下端拴一质量为m的物块,物块放在光滑斜面上的P点并保持静止,弹簧与斜面平行,此时弹簧具有的弹性势能为EP.已知弹簧的劲度系数为k.现将物块缓慢沿斜面向上移动,到弹簧刚恢复至原长位置时,由静止释放物块.求:在以后的运动过程中物块的最大的速度.
如图所示,倾角为θ的直角斜面体固定在水平地面上,一根轻质弹簧上端固定在斜面上,下端拴一质量为m的物块,物块放在光滑斜面上的P点并保持静止,弹簧与斜面平行,此时弹簧具有的弹性势能为EP.已知弹簧的劲度系数为k.现将物块缓慢沿斜面向上移动,到弹簧刚恢复至原长位置时,由静止释放物块.求:在以后的运动过程中物块的最大的速度. 位于竖直平面内矩形平面导线框abcd.水平边ab长L1=1.0m,竖直边ad长L2=0.5m,线框的质量m=0.2kg,线框的电阻R=2Ω,其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行.两边界间距离为H,H>L2,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域上边界PP′的距离为h=0.7m处自由下落.已知线框dc进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已到达这一段的最大值.问从线框开始下落到dc边刚刚到达磁场区域下边界QQ′过程中,线框克服安培力做的总功为多少?(取g=10m/s2,不计空气阻力)
位于竖直平面内矩形平面导线框abcd.水平边ab长L1=1.0m,竖直边ad长L2=0.5m,线框的质量m=0.2kg,线框的电阻R=2Ω,其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行.两边界间距离为H,H>L2,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域上边界PP′的距离为h=0.7m处自由下落.已知线框dc进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已到达这一段的最大值.问从线框开始下落到dc边刚刚到达磁场区域下边界QQ′过程中,线框克服安培力做的总功为多少?(取g=10m/s2,不计空气阻力)