题目内容
11.一质量m=4kg的小木块以V0=3m/s的速度,经过一光滑球面的顶端,已知球面的半径R=2m,求小木块的向心加速度和小木块对球面的压力.(g=10m/s2)分析 木块做半径是R=2m的圆周运动,根据向心加速度公式a=$\frac{{v}^{2}}{R}$求出向心加速度.
经过一光滑球面的顶端,木块受到重力和支持力两个力,由其合力提供其向心力,根据牛顿第二定律求解球面对木块的支持力,再由牛顿第三定律求木块对球面的压力.
解答 解:小木块的向心加速度为:
a=$\frac{{v}_{0}^{2}}{R}$=$\frac{{3}^{2}}{2}$=4.5m/s2.
根据牛顿第二定律得:
mg-N=ma
解得:N=m(g-a)=4×(10-4.5)N=22N
由牛顿第三定律得知小木块对球面的压力大小为:N′=N=22N,方向竖直向下
答:小木块的向心加速度为4.5m/s2.小木块对球面的压力大小为22N,方向竖直向下.
点评 圆周运动涉及力的问题就要考虑到向心力,圆周运动是由指向圆心的合力提供向心力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.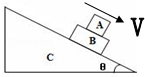 如图所示,固定斜面C上有A和B两个物体一起相对静止地沿斜面匀速下滑,请分析A、B两个物体受力的个数分别为( )
如图所示,固定斜面C上有A和B两个物体一起相对静止地沿斜面匀速下滑,请分析A、B两个物体受力的个数分别为( )
 如图所示,固定斜面C上有A和B两个物体一起相对静止地沿斜面匀速下滑,请分析A、B两个物体受力的个数分别为( )
如图所示,固定斜面C上有A和B两个物体一起相对静止地沿斜面匀速下滑,请分析A、B两个物体受力的个数分别为( )| A. | 3个,4个 | B. | 3个,5个 | C. | 3个,6个 | D. | 4个,5个 |
6.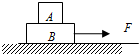 如图所示,A、B两物体叠放在一起,静放在水平地面上,在水平拉力F的作用下,两者相对静止一起向右做匀加速直线运动,则下列说法正确的是( )
如图所示,A、B两物体叠放在一起,静放在水平地面上,在水平拉力F的作用下,两者相对静止一起向右做匀加速直线运动,则下列说法正确的是( )
 如图所示,A、B两物体叠放在一起,静放在水平地面上,在水平拉力F的作用下,两者相对静止一起向右做匀加速直线运动,则下列说法正确的是( )
如图所示,A、B两物体叠放在一起,静放在水平地面上,在水平拉力F的作用下,两者相对静止一起向右做匀加速直线运动,则下列说法正确的是( )| A. | B对A的支持力对A不做功 | B. | B对A的摩擦力对A不做功 | ||
| C. | B对A的摩擦力对A做负功 | D. | B对A的摩擦力对A做正功 |
3. 如图,物体A在两个相互垂直的力F1和F2 作用下运动,在一段时间内,F1 对物体做功4J,F2对A做功3J,那么合力做功是( )
如图,物体A在两个相互垂直的力F1和F2 作用下运动,在一段时间内,F1 对物体做功4J,F2对A做功3J,那么合力做功是( )
 如图,物体A在两个相互垂直的力F1和F2 作用下运动,在一段时间内,F1 对物体做功4J,F2对A做功3J,那么合力做功是( )
如图,物体A在两个相互垂直的力F1和F2 作用下运动,在一段时间内,F1 对物体做功4J,F2对A做功3J,那么合力做功是( )| A. | 5J | B. | 7J | ||
| C. | 1J | D. | F1、F2大小未知故无法确定 |
13. 如图甲为两种光以相同的入射角从某种介质射向真空时的光路图.图乙为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,则下列说法正确的是( )
如图甲为两种光以相同的入射角从某种介质射向真空时的光路图.图乙为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,则下列说法正确的是( )
 如图甲为两种光以相同的入射角从某种介质射向真空时的光路图.图乙为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,则下列说法正确的是( )
如图甲为两种光以相同的入射角从某种介质射向真空时的光路图.图乙为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,则下列说法正确的是( )| A. | 由图甲可知,a光的全反射临界角小于b光的全反射临界角 | |
| B. | 通过图乙中的双缝干涉装置,a光的干涉条纹间距比b光的窄 | |
| C. | 在其它条件不变的情况下,若将D屏向右平移一段距离,则屏上干涉条纹间距将变大 | |
| D. | 由实验观察和P1为a光的第一级亮纹的中心,在其它条件不变的情况下,若将D屏向右平移一段距离,屏上P1位置仍然为a光的亮纹的中心 |
 如图所示,A为带正电Q的金属板,小球的质量为m、电荷量为q,用绝缘丝线悬挂于O点.小球由于受水平向右的电场力而静止在沿金属板的垂直平分线上距板为r的位置,悬线与竖直方向的夹角为θ.试求小球所在处的场强.
如图所示,A为带正电Q的金属板,小球的质量为m、电荷量为q,用绝缘丝线悬挂于O点.小球由于受水平向右的电场力而静止在沿金属板的垂直平分线上距板为r的位置,悬线与竖直方向的夹角为θ.试求小球所在处的场强.