题目内容
15. 一位同学做“探究单摆周期与摆长的关系”的实验,他将摆球挂起后,进行了如下步骤:
一位同学做“探究单摆周期与摆长的关系”的实验,他将摆球挂起后,进行了如下步骤:A.测摆长L:用米尺量出摆线长度;
B.测周期T:将摆球拉起一个小角度,然后放开,在摆球某次通过最低点时,按下秒表开始计时,同时将此次通过最低点作为第一次,接着一直数到摆球第60次通过最低点时,按秒表停止计时,读出这段时间t,计算出单摆的振动周期T=$\frac{t}{60}$;
C.改变摆长,重复上述步骤几次;
D.数据分析:.该同学经实验测量得到一组数据,如表所示:
| 摆长L(m) | 0.800 | 0.90 | 1.000 | 1.100 | 1.200 |
| 周期T(s) | 1.79 | 1.90 | 2.00 | 2.10 | 2.20 |
| T2(s2) | 3.20 | 3.61 | 4.00 | 4.41 | 4.84 |
(2)指出上面A、B步骤中遗漏或错误的地方:
①步骤A中应用游标卡尺测出摆球直径,摆长应为摆线长加上摆球的半径
②步骤B中单摆周期T计算式应是$T=\frac{t}{29.5}$..
分析 (1)根据实验原理由单摆周期公式变形,得到T2与L的关系式,分析图象斜率的意义;
(2)①摆长等于悬点到球心的距离;
②小球通过最低点作为第一次时开始计时,接着一直数到摆球第60次通过最低点时,为29.5个周期.
解答  解:(1)将表格中的数据在坐标纸上描点,然后连线如图,
解:(1)将表格中的数据在坐标纸上描点,然后连线如图,
由图可知,T2与摆线的长度L成正比,即T2∝L.
(2)①步骤A、摆长不等于摆线的长度,所以要用卡尺测出摆球直径d,摆长L等于摆线长与$\frac{d}{2}$之和;
②步骤B、小球通过最低点作为第一次时开始计时,接着一直数到摆球第60次通过最低点时,为29.5个周期,所以周期:$T=\frac{t}{29.5}$.
故答案为:(1)T2∝L;(2)①步骤A中应用游标卡尺测出摆球直径,摆长应为摆线长加上摆球的半径;②步骤B中单摆周期T计算式应是$T=\frac{t}{29.5}$.(或指出周期测量错误即可)
点评 本题关键明确实验原理,然后从实验原理出发选择有利于减小误差的器材,判断误差情况,基础题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
5.利用如图1所示的电路测定电源电动势和内电阻,提供的器材有:

A.干电池两节(每节电动势约1.5V,内阻未知)
B.直流电压表V1、V2(内阻很大)
C.直流电流表A(内阻可以忽略不计)
D.定值电阻R(阻值未知,但不小于5Ω)
E.滑动变阻器
F.导线和开关
(1)甲同学利用该电路完成实验时,由于某根导线发生断路故障,因此只记录到了一个电压表和电流表的示数,如下表所示:
试利用表格中的数据在所给的坐标图如图2中作出U-I图,由图象可知,该同学测得两节干电池总的电动势为2.90V,总内阻为3.50Ω.由计算得到的数据可以判断能够正确读数的电压表应该为表V1(填“V1”或“V2”)
(2)乙同学在找出断路的导线并调换好的导线后,连接该电路继续实验时,由于电流表发生短路故障,因此只能记录下两个电压表示数,该同学利用记录的数据,以表V2示数U2为横坐标,表V1示数U1为纵坐标作图象,也得到一条不过原点的直线,已知直线的斜率为k,纵轴截距为b,则两节干电池总的电动势大小为$\frac{b}{1-k}$,两节干电池总的内阻不可以(填“可以”或“不可以”)求出.如果该同学希望通过利用图象的截距直接得到电源的电动势,保持U1为纵坐标不变,应该选用U1-U2作为横坐标作图.

A.干电池两节(每节电动势约1.5V,内阻未知)
B.直流电压表V1、V2(内阻很大)
C.直流电流表A(内阻可以忽略不计)
D.定值电阻R(阻值未知,但不小于5Ω)
E.滑动变阻器
F.导线和开关
(1)甲同学利用该电路完成实验时,由于某根导线发生断路故障,因此只记录到了一个电压表和电流表的示数,如下表所示:
| $\frac{U}{V}$ | 2.62 | 2.48 | 2.34 | 2.20 | 2.06 | 1.92 |
| $\frac{I}{A}$ | 0.08 | 0.12 | 0.19 | 0.20 | 0.24 | 0.28 |
(2)乙同学在找出断路的导线并调换好的导线后,连接该电路继续实验时,由于电流表发生短路故障,因此只能记录下两个电压表示数,该同学利用记录的数据,以表V2示数U2为横坐标,表V1示数U1为纵坐标作图象,也得到一条不过原点的直线,已知直线的斜率为k,纵轴截距为b,则两节干电池总的电动势大小为$\frac{b}{1-k}$,两节干电池总的内阻不可以(填“可以”或“不可以”)求出.如果该同学希望通过利用图象的截距直接得到电源的电动势,保持U1为纵坐标不变,应该选用U1-U2作为横坐标作图.
6. 细光束AO中含有a、b两种频率的光.细光束AO以45°的入射角从某种介质射向空气时,沿不同传播方向分成两部分,如图所示.若a光频率为ν1,b光频率为v2,关于这两种单色光,下列说法中正确的是( )
细光束AO中含有a、b两种频率的光.细光束AO以45°的入射角从某种介质射向空气时,沿不同传播方向分成两部分,如图所示.若a光频率为ν1,b光频率为v2,关于这两种单色光,下列说法中正确的是( )
 细光束AO中含有a、b两种频率的光.细光束AO以45°的入射角从某种介质射向空气时,沿不同传播方向分成两部分,如图所示.若a光频率为ν1,b光频率为v2,关于这两种单色光,下列说法中正确的是( )
细光束AO中含有a、b两种频率的光.细光束AO以45°的入射角从某种介质射向空气时,沿不同传播方向分成两部分,如图所示.若a光频率为ν1,b光频率为v2,关于这两种单色光,下列说法中正确的是( )| A. | 从该介质射向空气时,a光发生全反射时的临界角一定大于45° | |
| B. | 该介质对b光的折射率一定小于$\sqrt{2}$ | |
| C. | 用a光和b光分别做双缝干涉实验,若实验条件相同则b光在屏上形成的明条纹的间距较小 | |
| D. | a光、b光照射入某介质,b光的传播速度小些 |
10.某宇航员要到离地球5光年的星球上去旅行,如果希望把这路程缩短为3光年,则他所乘坐的飞船相对地球的速度为( )
| A. | 0.5C | B. | 0.6C | C. | 0.8C | D. | 0.9C |
4.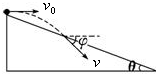 如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角为Φ,速度方向与斜面的夹角为α.下列说法中正确的是( )
如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角为Φ,速度方向与斜面的夹角为α.下列说法中正确的是( )
 如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角为Φ,速度方向与斜面的夹角为α.下列说法中正确的是( )
如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角为Φ,速度方向与斜面的夹角为α.下列说法中正确的是( )| A. | θ和Φ的关系式为tanΦ=sinθ | B. | θ和Φ的关系式为tanΦ=2tanθ | ||
| C. | 若平抛的初速度增大,则α将增大 | D. | 若平抛的初速度增大,则α将减小 |
5.在研究下列运动时,能将人或物体看做质点的是( )
| A. | 研究地球的自转形成白天和黑夜时 | B. | 研究车轮的转动时 | ||
| C. | 研究万米冠军在长跑中的位置时 | D. | 研究花样滑冰运动员的美妙姿态时 |
 为了测一个额定电压为100V的灯泡的额定功率,设计了如图所示的电路.滑动变阻器的阻值范围是0~100Ω,原、副线圈的匝数比为2:1.灯泡正常发光时,滑片恰好处于正中且电流表A的示数为1.2A.
为了测一个额定电压为100V的灯泡的额定功率,设计了如图所示的电路.滑动变阻器的阻值范围是0~100Ω,原、副线圈的匝数比为2:1.灯泡正常发光时,滑片恰好处于正中且电流表A的示数为1.2A. 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.