Question

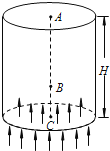
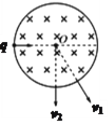
【题目】如图所示为圆柱形区域的横截面，在该区域加沿圆柱轴线方向的匀强磁场。带电粒子（不计重力）第一次以速度v1沿截面直径入射，粒子飞入磁场区域时，速度方向偏转60°角；该带电粒子第二次以速度v2从同一点沿同一方向入射，粒子飞出磁场区域时，速度方向偏转90°角。则带电粒子第一次和第二次在磁场中运动的半径之比为_______； 速度之比为__________；周期之比为_________；时间之比为__________。

Answer 1

【答案】：1 ：1 1:1 2：3

【解析】

粒子进入磁场时，受到洛伦兹力作用而做匀速圆周运动，速度的偏向角等于轨迹对应的圆心角，再可求出轨迹对应的圆心角，由求解时间之比；根据几何知识求出轨迹半径之比，由半径公式求出速度之比．

设圆柱形区域为R。带电粒子第一次以速度沿直径入射时，轨迹如图所示：

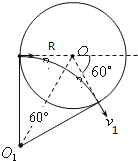
粒子飞出此磁场区域时速度方向偏转60°角，则知带电粒子轨迹对应的圆心角，轨迹半径为，运动时间为，带电粒子第二次以速度沿直径入射时，粒子飞出此磁场区域时速度方向偏转90°角，则知带电粒子轨迹对应的圆心角，轨迹半径为，运动时间为，所以轨迹半径之比：，时间之比：，根据半径公式，得速度之比：，根据可知，周期之比为1：1。