题目内容
 如图所示,A、B、C三个物体质量均为m,其中厚度相同的A、B位于光滑的水平面上,可视为质点的小物块C放在静止的B物体上,物体A以速度v0.向物体B运动,与B发生碰撞(碰撞时间极短),碰后A、B以相同的速度运动,但互不粘连;C滑过B后又在A上滑行,最后停在A上,与A一起以
如图所示,A、B、C三个物体质量均为m,其中厚度相同的A、B位于光滑的水平面上,可视为质点的小物块C放在静止的B物体上,物体A以速度v0.向物体B运动,与B发生碰撞(碰撞时间极短),碰后A、B以相同的速度运动,但互不粘连;C滑过B后又在A上滑行,最后停在A上,与A一起以| 3 | 10 |
(1)物体B最终的速度;
(2)小物块C在物体A和物体B上滑行过程中由于摩擦产生的热量之比.
分析:对ABC组成的系统全过程由动量守恒定律求解物体B最终的速度.
先分析AB碰撞过程,根据动量守恒列式,对ABC组成的系统由动量守恒定律求得C离开B的瞬时速度.
由能量关系求得该过程中C在B上滑行由于摩擦产生的热量.
对A、C组成的系统由动量守恒求得C和A相互作用至达到共同速度.
由能量关系求得该过程中C在A上滑行由于摩擦产生的热量.
先分析AB碰撞过程,根据动量守恒列式,对ABC组成的系统由动量守恒定律求得C离开B的瞬时速度.
由能量关系求得该过程中C在B上滑行由于摩擦产生的热量.
对A、C组成的系统由动量守恒求得C和A相互作用至达到共同速度.
由能量关系求得该过程中C在A上滑行由于摩擦产生的热量.
解答:解:(1)从最初A以速度υ0运动到最终AC以共同速度υ4运动、同时B以速度υ2匀速运动的过程中,
对ABC组成的系统全过程由动量守恒定律有:mv0=(m+m)v4+mv2
求得:v2=
v0
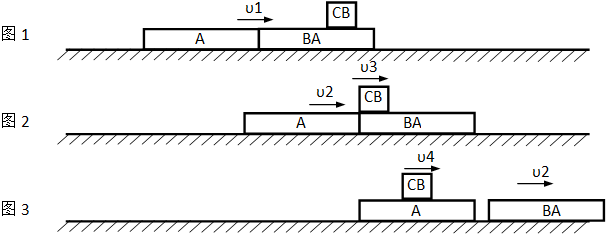
(2)如图1,从A以速度υ0运动到与B相碰获得共同速度(设为υ1)的过程中,
对AB组成的系统由动量守恒定律得:mv0=(m+m)v1
设C离开B的瞬时速度为υ3,AB整体的速度减小为υ2,如图2所示,
对ABC组成的系统由动量守恒定律得:(m+m)v1=(m+m)v2+mv3
设该过程中C在B上滑行由于摩擦产生的热量为QB,
由能量关系可得:
(m+m)
=
(m+m)
+
m
+QB
C以速度υ3离开B滑上A后,AB分离,B以速度υ2匀速运动,C和A相互作用至达到共同速度υ4,如图3所示.
该过程中对A、C组成的系统由动量守恒定律有mv2+mv3=(m+m)v4
设该过程中C在A上滑行由于摩擦产生的热量为QA,由功能关系可得:
m
+
m
=
(m+m)
+QA
联立以上各式及题中已知v4=
v0,
可得:
=
.
答:(1)物体B最终的速度是
v0;
(2)小物块C在物体A和物体B上滑行过程中由于摩擦产生的热量之比是
.
对ABC组成的系统全过程由动量守恒定律有:mv0=(m+m)v4+mv2
求得:v2=
| 2 |
| 5 |
(2)如图1,从A以速度υ0运动到与B相碰获得共同速度(设为υ1)的过程中,
对AB组成的系统由动量守恒定律得:mv0=(m+m)v1
设C离开B的瞬时速度为υ3,AB整体的速度减小为υ2,如图2所示,
对ABC组成的系统由动量守恒定律得:(m+m)v1=(m+m)v2+mv3
设该过程中C在B上滑行由于摩擦产生的热量为QB,
由能量关系可得:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
C以速度υ3离开B滑上A后,AB分离,B以速度υ2匀速运动,C和A相互作用至达到共同速度υ4,如图3所示.
该过程中对A、C组成的系统由动量守恒定律有mv2+mv3=(m+m)v4
设该过程中C在A上滑行由于摩擦产生的热量为QA,由功能关系可得:
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| v | 2 4 |
联立以上各式及题中已知v4=
| 3 |
| 10 |
可得:
| QA |
| QB |
| 1 |
| 7 |

答:(1)物体B最终的速度是
| 2 |
| 5 |
(2)小物块C在物体A和物体B上滑行过程中由于摩擦产生的热量之比是
| 1 |
| 7 |
点评:本题要注意物体的运动过程及临界条件的确定,由题意可得出.
先依次分析,找出物体运动过程.同一个问题可能会选择不同的系统作为研究对象.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.
先依次分析,找出物体运动过程.同一个问题可能会选择不同的系统作为研究对象.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )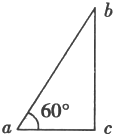 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,