题目内容
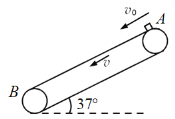
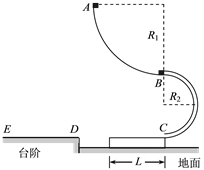
【题目】如图所示,半径为![]() =1.8m的1/4光滑圆弧与半径为
=1.8m的1/4光滑圆弧与半径为![]() =0.3m的半圆光滑细管平滑连接并固定,光滑水平地面上紧靠管口有一长度为
=0.3m的半圆光滑细管平滑连接并固定,光滑水平地面上紧靠管口有一长度为![]() =2.0m、质量为M=1.5kg的木板,木板上表面正好与管口底部相切,处在同一水平线上,木板的左方有一足够长的台阶,其高度正好与木板相同.现在让质量为
=2.0m、质量为M=1.5kg的木板,木板上表面正好与管口底部相切,处在同一水平线上,木板的左方有一足够长的台阶,其高度正好与木板相同.现在让质量为![]() =2kg的物块静止于B处,质量为
=2kg的物块静止于B处,质量为![]() =1kg的物块从光滑圆弧顶部的A处由静止释放,物块
=1kg的物块从光滑圆弧顶部的A处由静止释放,物块![]() 下滑至B处和
下滑至B处和![]() 碰撞后不再分开,整体设为物块m(m=
碰撞后不再分开,整体设为物块m(m=![]() +
+![]() ).物块m越过半圆管底部C处滑上木板使其从静止开始向左运动,当木板速度为2m/s时,木板与台阶碰撞立即被粘住(即速度变为零),若
).物块m越过半圆管底部C处滑上木板使其从静止开始向左运动,当木板速度为2m/s时,木板与台阶碰撞立即被粘住(即速度变为零),若![]() ,物块碰撞前后均可视为质点,圆管粗细不计.
,物块碰撞前后均可视为质点,圆管粗细不计.
(1)求物块![]() 和
和![]() 碰撞过程中损失的机械能;
碰撞过程中损失的机械能;
(2)求物块m滑到半圆管底部C处时所受支持力大小;
(3)若物块m与木板及台阶表面间的动摩擦因数均为![]() =0.25,求物块m在台阶表面上滑行的最大距离.
=0.25,求物块m在台阶表面上滑行的最大距离.
【答案】⑴12J ⑵190N ⑶0.8m
【解析】试题分析:(1)选由机械能守恒求出物块![]() 下滑到B点时的速度;
下滑到B点时的速度; ![]() 、
、![]() 碰撞满足动量守恒,由
碰撞满足动量守恒,由![]() 求出碰撞过程中损失的机械能;(2)物块m由B到C满足机械能守恒,在C点由牛顿第二定律可求出物块m滑到半圆管底部C处时所受支持力大小;(3)根据动量守恒定律和动能定理列式即可求解.
求出碰撞过程中损失的机械能;(2)物块m由B到C满足机械能守恒,在C点由牛顿第二定律可求出物块m滑到半圆管底部C处时所受支持力大小;(3)根据动量守恒定律和动能定理列式即可求解.
⑴设物块![]() 下滑到B点时的速度为
下滑到B点时的速度为![]() ,由机械能守恒可得:
,由机械能守恒可得:
![]()
解得: ![]()
![]() 、
、![]() 碰撞满足动量守恒:
碰撞满足动量守恒: ![]()
解得; ![]()
则碰撞过程中损失的机械能为: ![]()
⑵物块m由B到C满足机械能守恒: ![]()
解得: ![]()
在C处由牛顿第二运动定律可得: ![]()
解得: ![]()
⑶设物块m滑上木板后,当木板速度为![]() 时,物块速度为
时,物块速度为![]() ,
,
由动量守恒定律得: ![]()
解得: ![]()
设在此过程中物块运动的位移为![]() ,木板运动的位移为
,木板运动的位移为![]() ,由动能定理得:
,由动能定理得:
对物块m: ![]()
解得: ![]()
对木板M: ![]()
解得: ![]()
此时木板静止,物块m到木板左端的距离为: ![]()
设物块m在台阶上运动的最大距离为![]() ,由动能定理得:
,由动能定理得:
![]()
解得: ![]()