题目内容
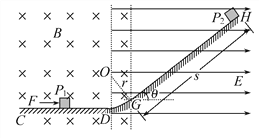
【题目】在如图所示的竖直平面内,水平轨道CD和倾斜轨道GH与半径r=![]() m的光滑圆弧轨道分别相切于D点和G点,GH与水平面的夹角θ=37°。过G点、垂直于纸面的竖直平面左侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度B=1.25T;过D点、垂直于纸面的竖直平面右侧有匀强电场,电场方向水平向右,电场强度E=1×104N/C。小物体P1质量m=2×10-3kg、电荷量q=+8×10-6C,受到水平向右的推力F=9.98×10-3N的作用,沿CD向右做匀速直线运动,到达D点后撤去推力。当P1到达倾斜轨道底端G点时,不带电的小物体P2在GH顶端静止释放,经过时间t=0.1s与P1相遇。P1和P2与轨道CD、GH间的动摩擦因数均为μ=0.5,取g=10m/s2,sin37°=0.6,cos37°=0.8,物体电荷量保持不变,不计空气阻力。求:
m的光滑圆弧轨道分别相切于D点和G点,GH与水平面的夹角θ=37°。过G点、垂直于纸面的竖直平面左侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度B=1.25T;过D点、垂直于纸面的竖直平面右侧有匀强电场,电场方向水平向右,电场强度E=1×104N/C。小物体P1质量m=2×10-3kg、电荷量q=+8×10-6C,受到水平向右的推力F=9.98×10-3N的作用,沿CD向右做匀速直线运动,到达D点后撤去推力。当P1到达倾斜轨道底端G点时,不带电的小物体P2在GH顶端静止释放,经过时间t=0.1s与P1相遇。P1和P2与轨道CD、GH间的动摩擦因数均为μ=0.5,取g=10m/s2,sin37°=0.6,cos37°=0.8,物体电荷量保持不变,不计空气阻力。求:
(1)小物体P1在水平轨道CD上运动速度v的大小;
(2)倾斜轨道GH的长度s。
【答案】(1)4m/s(2)0.56m
【解析】试题分析: (1)设小物体P1在匀强磁场中运动的速度为v,受到水平外力F,重力mg,支持力N,竖直向上的洛伦兹力F1,滑动摩擦力f
则F1=qvB①
![]() ,
,![]() ②
②
匀速直线运动,物体处于平衡状态;![]() ③
③
解得![]() m/s④
m/s④
说明:①③各1分,②④各2分
(2)设物体P1在G点的速度为![]() ,由于洛伦兹力不做功
,由于洛伦兹力不做功
由动能定理知![]() ⑤
⑤
解得速度![]() m/s
m/s
小物体P1在GH上运动受到水平向右的电场力qE,重力mg,垂直斜面支持力N1,沿斜面向下的滑动摩擦力f1设加速度为![]()
由牛顿第二定律有![]() ,
,![]()
![]() ,⑥
,⑥
解得![]() m/s2
m/s2
小物体P1在GH上匀加速向上运动![]() =0.55m⑦
=0.55m⑦
小物体P2在GH上运动受到重力m2g,垂直斜面支持力N2,沿斜面向上的滑动摩擦力f2,加速度为![]()
则![]() ⑧
⑧
解得![]() m/s2
m/s2
小物体P2在GH上匀加速向下运动![]() =0.01m⑨
=0.01m⑨
故轨道长![]() ⑩
⑩
所以s="0.56m" ⑾
说明:⑦⑧⑨⑩各1分,⑥⑾各2分,⑤式3分