题目内容
15. 如图,光滑水平地面上有一固定墙壁,紧靠墙面左侧停放一长为L=1m,质量为M=0.2kg的长木板,在距长木板左端为kL(0<k<0.5)处放置着A、B两小木块,A、B质量均为m=0.2kg.某时刻,A、B在强大内力作用下突然分开,分开瞬间A的速度为vA=4m/s,方向水平向左. B与墙壁碰撞瞬间不损失机械能,A、B与长木板间的动摩擦因数分别为μA=0.2和μB=0.3.
如图,光滑水平地面上有一固定墙壁,紧靠墙面左侧停放一长为L=1m,质量为M=0.2kg的长木板,在距长木板左端为kL(0<k<0.5)处放置着A、B两小木块,A、B质量均为m=0.2kg.某时刻,A、B在强大内力作用下突然分开,分开瞬间A的速度为vA=4m/s,方向水平向左. B与墙壁碰撞瞬间不损失机械能,A、B与长木板间的动摩擦因数分别为μA=0.2和μB=0.3.(1)求AB分离瞬间,B的速度v1;
(2)若k=0.39,求A离开木板时,B的速度大小v2;
(3)若最终B能够相对木板静止,则k应满足什么条件,并求出最终B所停位置距木板左端距离s和k的关系式.
分析 (1)在A、B分离瞬间,A、B系统动量守恒,根据动量守恒定律求解;
(2)在A离开木板前,B对木板向右的摩擦力大于A对木板向左的摩擦力,所以此时木板处于静止状态.对A,从与B分离到离开木板过程中,做匀减速直线运动,根据牛顿第二定律求解加速度,再结合运动学基本公式求解;
(3)先根据动能定理判断B能不能在撞墙前停止,再根据木板与B构成的系统动量守恒、能量守恒列式求解.
解答 解:(1)在A、B分离瞬间,A、B系统动量守恒,有
mvA=mv1
解得:v1=4m/s
(2)在A离开木板前,B对木板向右的摩擦力大于A对木板向左的摩擦力,所以此时木板处于静止状态.对A,从与B分离到离开木板过程中,做匀减速直线运动,有
μAmg=maA
解得:${a}_{A}=2m/{s}^{2}$
根据运动学基本公式得:
$kL={v}_{A}t-\frac{1}{2}{a}_{A}{t}^{2}$
解得:t=0.1s
此过程中,B与A的运动时间相同,假设此时B还没有撞到墙壁.有
μBmg=maB
解得:${a}_{B}=3m/{s}^{2}$
根据v2=v1-aBt
解得:v2=3.7m/s
而${s}_{B}=\frac{{v}_{1}+{v}_{2}}{2}t=0.385m<(1-k)L$
假设成立,即此时B速度为v2=3.7m/s
(3)假设B能在撞到墙壁前停止,则有:
$-{μ}_{B}mgs=0-\frac{1}{2}m{{v}_{1}}^{2}$
解得 s=5.3m>L,即B不可能在撞墙前停止.
B撞到墙壁前瞬间速度为vB,则:
$-{μ}_{B}mg(1-k)L=\frac{1}{2}m{{v}_{B}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$
B撞墙以后后,若B刚好不滑落,则B滑至木板左端时恰好最终达到共同速度v,木板与B构成的系统动量守恒、能量守恒,有
mvB=(m+M)v,
$\frac{1}{2}m{{v}_{B}}^{2}=\frac{1}{2}(m+M){{v}_{\;}}^{2}+{μ}_{B}mgL$
解得$k=\frac{1}{3}$
即若木块B不从木板上滑落,需要满足:$k≤\frac{1}{3}$
若停在距左端为S处,则对木板与B,由能量守恒得:
$\frac{1}{2}m{{v}_{B}}^{2}=\frac{1}{2}(m+M){{v}_{\;}}^{2}+{μ}_{B}mg(L-s)$
解得 $s=\frac{1}{6}-\frac{k}{2}$,即最终物块B停在距左端为$s=\frac{1}{6}-\frac{k}{2}$处.
答:(1)AB分离瞬间,B的速度v1为4m/s;
(2)若k=0.39,求A离开木板时,B的速度大小v2为3.7m/s;
(3)若最终B能够相对木板静止,则k应满足$k≤\frac{1}{3}$,最终B所停位置距木板左端距离s和k的关系式为$s=\frac{1}{6}-\frac{k}{2}$.
点评 本题综合运用了动量守恒定律、能量守恒定律、动能定理、牛顿第二定律及运动学基本公式,关键是正确分析木块和木板的受力情况和运动情况,能选择合适的定理求解,难度较大.

 2013年6月10日上午,我国首次太空授课在距地球300多千米的“天空一号”上举行,如图所示的是宇航员王亚萍在“天空一号”上所做的“水球”.下列关于“水球”和“天空一号”的说法正确的是( )
2013年6月10日上午,我国首次太空授课在距地球300多千米的“天空一号”上举行,如图所示的是宇航员王亚萍在“天空一号”上所做的“水球”.下列关于“水球”和“天空一号”的说法正确的是( )| A. | “水球”的形成是因为太空中没有重力 | |
| B. | “水球”的向心加速度小于5m/s2 | |
| C. | “天空一号”运行速度小于7.9km/s | |
| D. | “天宫一号”的角速度比同步卫星的大 |

| A. | B卫星比A卫星运行周期小 | |
| B. | A卫星在图示位置加速后有可能会撞上B卫星 | |
| C. | A卫星的运行速度一定小于地球的第一宇宙速度 | |
| D. | 可以通过A卫星的运行周期和万有引力常量计算出地球的质量 |
| A. | α射线与γ射线都是电磁波 | |
| B. | β射线为原子的核外电子电离后形成的电子流 | |
| C. | 用加温、加压或改变其化学状态的方法都不能改变放射性元素原子核衰变的半衰期 | |
| D. | 原子核经过衰变生成新核,新核的质量一定等于原核的质量,不可能出现质量亏损 |
 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中O~x2段是对称的曲线,x2~x3是直线段,则下列判断正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位移x变化的关系如图所示,其中O~x2段是对称的曲线,x2~x3是直线段,则下列判断正确的是( )| A. | x1处电场强度最大 | |
| B. | x2~x3段是匀强电场 | |
| C. | x1、x2、x3处电势φ1、φ2、φ3的关系为φ1>φ2>φ3 | |
| D. | 粒子在O~x2段做匀变速运动,x2~x3段做匀速直线运动 |
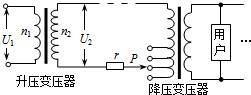 如图所示为某小型电站高压输电示意图.发电机输出功率恒定,升压变压器原、副线圈两端的电压分别为U1和U2.下列说法正确的是( )
如图所示为某小型电站高压输电示意图.发电机输出功率恒定,升压变压器原、副线圈两端的电压分别为U1和U2.下列说法正确的是( )| A. | 采用高压输电可以增大输电线中的电流 | |
| B. | 升压变压器原、副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{{U}_{2}}{{U}_{1}}$ | |
| C. | 输电线损耗的功率为$\frac{{{U}_{2}}^{2}}{r}$ | |
| D. | 将P上移,用户获得的电压将升高 |
 如图所示,一个U形导体框架,其宽度L=1m,框架平面与水平面夹角α=30°,其电阻可忽略不计,设匀强磁场的磁感应强度与U形框架的平面垂直.匀强磁场的磁感应强度B=0.2T.今有一条形导体AB,其质量为m=0.5kg,有效电阻R=0.1Ω,跨接在U形框架上,并能无摩擦地滑动.求:
如图所示,一个U形导体框架,其宽度L=1m,框架平面与水平面夹角α=30°,其电阻可忽略不计,设匀强磁场的磁感应强度与U形框架的平面垂直.匀强磁场的磁感应强度B=0.2T.今有一条形导体AB,其质量为m=0.5kg,有效电阻R=0.1Ω,跨接在U形框架上,并能无摩擦地滑动.求: